1)
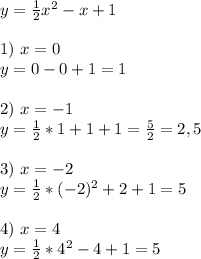
2)
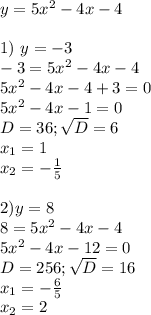
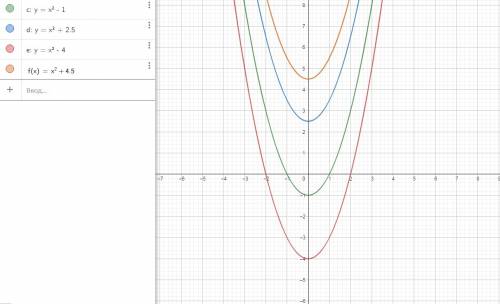
3)
1) y=x²+10 - парабола , поднятая на 10 точек вверх, координаты вершины (0;10)
2) y=x²-5 - парабола, на 5 точек вниз, координаты вершины (0;-5)
3) y=(x+7)² - парабола, передвинутая на 7 точек влево, вершина (-7;0)
4) y=(x-8)²-парабола, передвинутая на 8 точек вправо, вершина (8;0)
4) y=x²
1) y=x²+5
2)y=x²-4
3)y=(x-3)²
4)y=(x+6)²
5)
На фото, c Ox пересекается график функции y=x²-4.
Точки пересечения с Ox (-2;0) и (2;0)
И y=x²-1
Точки пересечения с Ox (-1;0) и (1;0)
С Oy : y=x²-1, (0;-1)
y=x²+2,5 , (0;2,5)
y=x²-4, (0;-4)
y=x²+4,5, (0;4,5)
Рассмотрим случаи, когда уравнение не квадратное. А именно, когда перед квадратом стоит коэффициент равен 0, и чтобы дискриминант был положительным. Т.е. a не должен быть равен 1, потому что он обращает коэффициент в 0 перед квадратом. Теперь выделим дискриминант этого уравнения:
А раз дискриминант должен быть положительным, то и выражение 8a-4 тоже.
Решаем неравенство:
ответ: a > 0.5