a) 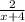
b) 
Объяснение:
Будем раскладывать на множиели при этой формулы :
ax² + bx +c = a(x - x₁)(x - x₂)
a) Для начала нам потребуется найти корни :
x² - x -20 = 0
{ x₁ + x₂ = 1 (система)
{ x₁ × x₂ = -20
x₁ = - 4
x₂ = 5
⇒ x² - x -20 = 1(x - (-4))(x - 5) = (x+4)(x-5)
Теперь подставляем это выражение в знаменатель, а также раскладываем на множители числитель :
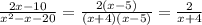
b) Так же, как и в примере, нам нужно найти корни, но уже двух многочленов : (x²+12x+27) и (x²+8x-9).
x² + 12x + 27 = 0
Буду решать через выделение полного квадрата :
(x + 6)² - 9 = 0
(x + 6)² = 9
x+6 = -3 x+6 = 3
x₁ = -9 x₂ = -3
⇒ x² + 12x + 27 = 1(x - (-9))(x - (-3)) = (x+9)(x+3)
Теперь разложим многочлен на множители, который в знаменателе :
x² + 8x - 9 = 0
Решаю опять же через выделение полного квадрата :
(x + 4)² - 25 = 0
(x + 4)² = 25
x+4 = -5 x+4 = 5
x₁ = -9 x₂ = 1
⇒ x² + 8x - 9 = 1(x - (-9))(x - 1) = (x+9)(x-1)
Теперь подставляем эти два выражения :
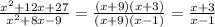
получим: t² - 2t + 1-а² = 0
D = 4 - 4(1-a²) > 0
4a² > 0
при a ≠ 0 существуют два корня
(t)1;2 = (2 +- √(4a²)) / 2 = 1 +- √(a²) = 1 +- |a|
но вопрос про корни (х)...
посмотрим еще и на (a+1)x^2-4x = t (t равно t1 или t2)
(a+1)x^2-4x - t = 0
D = 16 + 4*(a+1)*t
если D будет > 0, то уравнение при двух разных значениях (t)
получит 4 корня для х)))
значит, нужно выполнение условия D = 0
((тогда для t1 --один корень и для t2 --один корень)))
4*(a+1)*t = -16
(a+1)*t = -4
(a+1)*(1 +- |a|) = -4
по определению модуля это выражение будет выглядеть:
(a+1)*(1 +- a) = -4
знак + даст полный квадрат, который не может быть равен (-4)
остается случай с формулой разность квадратов...
a² = 5
a = +-√5
если сначала потребовать единственности корня для параметра (t)
D = 0 ⇒ 1-a² = 1 ⇒ a = 0
тогда t² - 2t + 1 = 0 ⇒ (t - 1)² = 0 ⇒ t = 1 = (a+1)x^2-4x ( и а = 0)))
x^2 - 4x - 1 = 0
D = 16 + 4 > 0 --условие существования двух корней)))
ответ: при а = 0, а = +-√5
(((вроде нигде не ошиблась)))