Воспользуемся стандартной формой записи квадратного уравнения y=ax²+bx+c для определения уравнения параболы, проходящей через три данные точки. Построим систему уравнений, заменяя значения x и y каждой точки в стандартной формуле квадратного уравнения, формируя систему из трех уравнений.
Если вершина находится в начале координат, то она имеет точку, симметричную заданной, это В(8; 4).
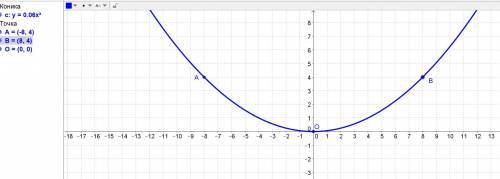
Поэтому имеем 3 точки на параболе: О(0; 0), А(-8; 4) и В(8; 4).
0 = a*0² + b*0 + c, отсюда с = 0.
4 = a*(-8)² + b*(-8) + 0,
4 = a*8² + b*8 + 0.
Сложим 2 последние уравнения:
8 = а*2*64, отсюда а = 8/(2*64) = 1/16.
Тогда b = (4 - a*8²)/8 = (4-(64/16))/8 = 0.
ответ: y=(1/16)x².
100 мандаринов.
Пошаговое объяснение:
Пусть мандарины раздавали детям, которых было х. Тогда, если раздавать их детям по 5 мандаринов каждому, то не хватит 4 мандаринов, а значит было мандаринов 5х - 4. В случае, если раздать по 4 мандарина, то в пакете останется 16 мандаринов: 4х + 16.
В двух случаях количество мандаринов равное:
5х - 4 = 4х + 16.
В правой части собираются слагаемые с неизвестной величиной, а в левой - свободные члены:
5х - 4х = 16 + 4.
х = 20 - детей получали мандарины.
В пакете было 4 * 20 + 16 = 100 мандаринов.
847*90=76230
76230+375=76605
Удачи))