1)P(X=0)=0,1*0,2*0,3=0,006
P(X=1)=0,9*0,2*0,3+0,1*0,8*0,3+0,1*0,2*0,7
P(X=2)=0,9*0,8*0,3+0,9*0,2*0,7+0,1*0,8*0,7
P(X=3)=0,9*0,8*0,7
2)ответ:
X 0 1 2 3 4
0,4096
0,4096
0,1536
0,0256
0,0016
3)Обозначим X - число опробованных ключей. Данная случайная величина может принимать следующие значения:
{X=1} - испробовали только один ключ (первый ключ является подходящим)
{X=2} - испробовали два ключа (первый ключ не подошел, второй ключ является искомым)
{X=3}- испробовали три ключа (первые два ключа не подошли, третий ключ является искомым)
{X=4]- испробовали четыре ключа (первые три ключа не подошли, четвертый ключ является искомым)
P(X=1) = 1/4
P(X=2) = 3/4*1/3 = 1/4
P(X=3) = 3/4*2/3*1/2 = 1/4
P(X=4) = 3/4*2/3*1/2*1 = 1/4
Ряд распределения случайной величины имеет вид
1 2 3 4
1/4 1/4 1/4 1/4
M(X) = 1*1/4 + 2*1/4 + 3*1/4 + 4*1/4 = 10/4
M(X^2) = 1*1/4 + 4*1/4 + 9*1/4+ 16*1/4 = 30/4
D(X) = M(X^2) - (M(X))^2 = 30/4 - 10/4 = 5
Функция распределения случайной величины имеет вид
{0, 0<=X<1
{1/4, 1<=X<2
F(X) = {2/4, 2<=X<3
{3/4, 3<=X<4
{0, X>=4
4)
Пошаговое объяснение:
а).
Пусть требуемое в задаче возможно и в ящике есть  ("маленьких") фруктов меньше
("маленьких") фруктов меньше 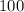 грамм. Тогда ("больших") фруктов, чья масса больше
грамм. Тогда ("больших") фруктов, чья масса больше
С одной стороны, масса всех фруктов равна 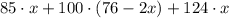 , а с другой стороны -
, а с другой стороны - 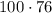 . Но так как мы говорим об одной и той же группе фруктов, то:
. Но так как мы говорим об одной и той же группе фруктов, то:
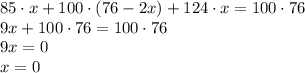
Но в задаче сказано, что "есть как минимум  различных по массе фрукта". Но полученный в этом случае результат противоречит условию Из этого заключаем, что описанная ситуация невозможна.
различных по массе фрукта". Но полученный в этом случае результат противоречит условию Из этого заключаем, что описанная ситуация невозможна.
ответ: нет, не может.
б).Пусть есть  "маленьких" фруктов и
"маленьких" фруктов и 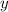 "больших" (в этом случае "средних" фруктов будет
"больших" (в этом случае "средних" фруктов будет 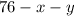 ). Точно также, как и в пункте, составим уравнение:
). Точно также, как и в пункте, составим уравнение:
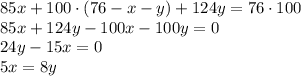
Мы получили очень интересный результат: в любом случае отношение количества "маленьких" и "больших" фруктов будет равно 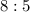 .
.
Значит, так как  и
и 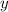 обязательно должны быть натуральными, общее число "маленьких" и "больших" фруктов должно делиться на
обязательно должны быть натуральными, общее число "маленьких" и "больших" фруктов должно делиться на 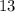 . Такое общее число будет обязательно меньше или равно
. Такое общее число будет обязательно меньше или равно 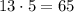 .
.
Получается, что количество "средних" фруктов больше или равно 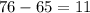 . В ящике их
. В ящике их 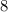 уж никак не может быть.
уж никак не может быть.
ответ: нет, не может.
в).Так как в задаче сказано "найдите наибольшую возможную массу фрукта", то наверняка нужно считать массы фруктов целыми числами.
Если есть 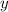 "больших" фруктов и
"больших" фруктов и 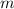 - масса наибольшего,то, чтобы "понизить" значение среднего арифметического (и привести его в итоге к числу
- масса наибольшего,то, чтобы "понизить" значение среднего арифметического (и привести его в итоге к числу 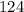 ), нужно массу остальных "больших" фруктов сделать как можно меньше - в районе
), нужно массу остальных "больших" фруктов сделать как можно меньше - в районе 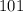 грамма.
грамма.
Поэтому:
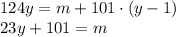
Как было фактически выяснено в пункте задачи, максимальное значение 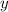 равно
равно 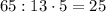 (а
(а 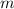 максимальное при максимальном значении
максимальное при максимальном значении 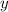 ).
).
Делаем вывод, что в этом случае:
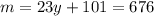 .
.
Теперь проверим, что этот случай нам действительно подходит:
Есть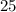 "больших" фруктов: масса
"больших" фруктов: масса 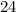 из них равна
из них равна 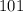 , а масса
, а масса  составляет
составляет 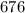 граммов.Есть
граммов.Есть 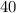 "маленьких" фруктов: масса каждого - по
"маленьких" фруктов: масса каждого - по 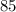 граммов.И еще
граммов.И еще  "средних" фруктов, ровно по
"средних" фруктов, ровно по 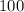 граммов.
граммов.Средняя масса "больших": 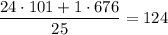 .
.
Средняя масса "средних": 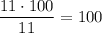 .
.
Средняя масса "маленьких": 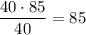 .
.
Общая средняя масса: 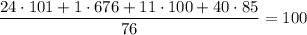 .
.
Все сходится!
ответ: 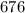 граммов.
граммов.
2)0,3:-1=-0,3
3)-0,3-0,1=-0,4