Натуральные: 7 , 201
Отрицательные целые: -8 , -21
Неотрицательные рациональные: 1.325 , 2.1
Иррациональные: 0.2020020002... , 3.(6) , 2.2360... , 2.718...
Теория:
Натуральные числа (от лат. naturalis «естественный») — числа, возникающие естественным образом при счёте (например, 1, 2, 3, 4, …)
Целые числа — расширение множества натуральных чисел, получаемое добавлением к нему нуля и отрицательных чисел.
Рациональное число (лат. ratio «отношение, деление, дробь») — число, которое можно представить обыкновенной дробью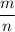 
, числитель 
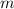— целое число, а знаменатель 
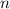— натуральное число.
Иррациона́льное число́ — это вещественное число, которое не является рациональным, то есть не может быть представлено в виде обыкновенной дроби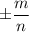 
, где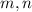 
— натуральные числа.
============
Не забывайте нажать " ", поставить оценку и, если ответ удовлетворил, то выберите его как "Лучший"
Успехов в учебе
Объяснение:
Смотрим на точки, каждая имеет по две координаты, первая координата по x а вторая по y.
Слева на право у нас идёт ось OX, и при этом возрастает, а OY возрастает снизу вверх.
Нам нужно определить расположение слева направо, и высота на которой они располагаются не важно, поэтому смотрим только на x.
На самом левом краю будет самая маленькая, с самым большим минусом, и по возрастанию:
C(-12 ; 7) самая малая по "х"
B(-6 ; 5)
K(-1 ) по умолчанию рядом с -1 у нас 0 по "y"
O(0) также здесь, это точка начала координат
A(5 ;6) а эта правее всех
cos(2x) = 1 - 2sin^2(x)
cos(π/2 - x) = sinx
1 - 2sin^2(x) - sinx -1 = 0
sinx*(2sinx + 1) = 0
1) sinx = 0
x = πk, k∈Z
2) 2sinx + 1 = 0
sinx = -1/2
x = -π/3 + 2πk, k∈Z
x = -2π/3 + 2πk, k∈Z
Определим, при каких k корни уравнения принадлежат отрезку [5π/2; 4π]
5π/2 ≤ πk ≤ 4π
2.5 ≤ k ≤ 4, k∈Z
k = 3, 4
x1 = 3π; x2 = 4π
5π/2 ≤ -π/3 + 2πk ≤ 4π
17π/6 ≤ 2πk ≤ 13π/3
17/12 ≤ k ≤ 13/6, k∈Z
k = 2
x3 = -π/3 + 4π = 11π/3
5π/2 ≤ -2π/3 + 2πk ≤ 4π
19π/6 ≤ 2πk ≤ 14π/3
19/12 ≤ k ≤ 14/6, k∈Z
k = 2
x4 = -2π/3 + 4π = 10π/3
ответ: 10π/3; 11π/3; 3π; 4π