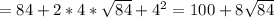
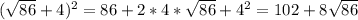
Объяснение:
1) y=x²-1 y=0 x=2
x²-1=0
x²=1 x₁=-1 x₂=1
S₁=₋₁∫¹(0-(x²-1)dx=₋₁∫¹(1-x²)dx=x-x³/3 ₋₁|¹=1-1³/3-(-1-(-1)³/3)=1-1/3-(-1+1/3)=
=2/3-(-2/3)=2/3+2/3=4/3≈1,33.
S₂=₁∫²(x²-1-0)dx=x³/3-x ₁|²=2³/3-2-(1³/3-1)=8/3-2-1/3+1=7/3-1=2¹/₃-1=1¹/₃=4/3≈1,33
S=S₁+S₂≈1,33+1,33≈2,66.
ответ: S≈2,66 кв.ед.
2) y=-x²-4x y=0, x=-3, x=-1
-x²-4x=0 |÷(-1)
x²+4x=0
x*(x+4)=0 x₁=-4 x₂=0
S=₋₃∫⁻¹(-x²-4x-0)dx=-x³/3-2x² ₋₃|⁻¹=-(-1)³/3-2*(-1)²-(-(-3)³/3-2*(-3)²)=
=1/3-2-9+18=7¹/₃≈7,33.
ответ: S≈7,33 кв. ед.
3) y=-8/x y=0 x₁=-4 x=-2
S=₋₄∫⁻²-(-8/x-0)dx=-8*lnx ₋₄|⁻²=-8*(ln(-2)-(8*ln(-4))=-8*ln(-2/-4)=
=-8*ln(1/2)=-8*ln(2⁻¹)=8*ln(2)≈8*0,693≈5,55.
ответ: S=5,55 кв. ед.
5) y=√(x+4) y=0 x₁=-3 x₂=5
S=₋₃⁵(√(x+4)-0)dx=((2/3)*(x+4)³/²) ₋₃|⁵=
=(2/3)*((5+4)³/²-(-3+4)³/²)=(2/3)*(9³/²-1³/²)=(2/3)*(27-1)=
=(2/3)*26=52/3=17¹/₃≈17,33.
ответ: S≈17,33 кв. ед.
Для вычисления корней данного кубического уравнения используются формулы Кардано.
Исходное уравнение приводится к виду: y^3+py+q=0.
Здесь применяются следующие формулы:
p=-b^2/(3a^2 )+c/a, q=(2b^3)/(27a^3 )-bc/(3a^2 )+d/a.
где
a - коэффициент при x^3,
b - коэффициент при x^2,
c - коэффициент при x,
d - свободный член.
Подставим наши значения в данные формулы, мы получим:
p = -3, q = 7.
Потом использовав формулу: Q = (p/3)³ + (q/2)², вычислим количество корней кубического уравнения. Если:
Q > 0 — один вещественный корень и два сопряженных комплексных корня;
Q < 0 — три вещественных корня;
Q = 0 — один однократный вещественный корень и один двукратный, или, если p = q = 0, то один трехкратный вещественный корень.
В нашем случае Q = 11,25, будем иметь один вещественный корень и два сопряженных комплексных корня.
А сами корни найдём по следующим формулам:
x1 = α + β − (b/3a);
x2,3 = −((α+β)/2) − (b/3a) ± i((α−β)/2)√3;
где α = (−(q/2) + √Q)^(1/3), β = (−(q/2) − √Q)^(1/3).
Подставив наши значения в выше указанные формулы вычислим что:
α = −0,5264, β = −1,8995
x1 = −4,42599; это вещественный корень.
x2,3 =−0,787 ± i·1.1891.