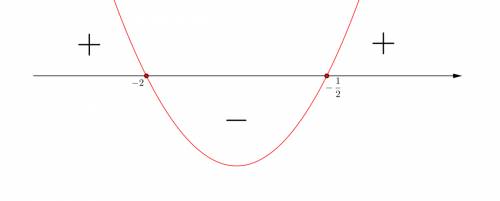
![5cosx+cos2x+3\geq0\\5cosx+2cos^2x-1+3\geq0\\2cos^2x+5cosx+2\geq0\\\\cosx=t\in[-1;\ 1]\\\\2t^2+5t+2\geq0\\\Delta_t=5^2-4\cdot2\cdot2=25-16=9;\ \sqrt{\Delta_t}=\sqrt9=3\\\\t_1=\frac{-5-3}{2\cdot2}=\frac{-8}{4}=-2;\ t_2=\frac{-5+3}{2\cdot2}=\frac{-2}{4}=-\frac{1}{2}\\\\\ [t\in(-\infty;-2]\ \cup\ [-\frac{1}{2};\ \infty)]\ \cap\ [-1;\ 1]=[-\frac{1}{2};\ 1]](/tpl/images/0279/7993/2215e.png)
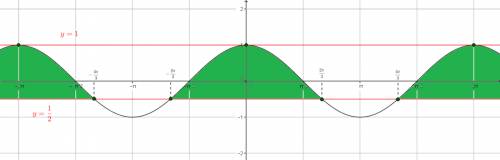
![-\frac{1}{2}\leq cosx\leq1\\\\cosx\geq-\frac{1}{2}\ \wedge\ cosx\leq1\\\\O:x\in[-\frac{2\pi}{3}+2k\pi;\ \frac{2\pi}{3}+2k\pi];\ k\in\mathbb{Z}](/tpl/images/0279/7993/e6252.png)

Cгруппируем слагаемые и используя формулу суммы кубов
а³+в³=(а+в)(а²-ав+в²), разложим на множители левую часть уравнения.
(x³+8)-(3x²+6x)=0; (х+2)(х²-2х+4)-3х*(х+2) =0;
(x+2)(x²-2x+4-3x)=0;
(x+2)(x²-5x+4)=0;
x+2=0; х=-2 или х²-5х+4=0 , ДЛЯ последнего УРАВНЕНИЯ
x₁·x₂=4
x₁+x₂=5, теперь просто подберите два числа, чтобы если их сложить, получить второй коэффициент, но с противоположным знаком, т.е. 5, а если перемножить, то получить свободный член с тем же знаком,т.е. 4, ясно, что это 1 и 4, т.к. 1+4=5; 1*4=4
ответ 1; 4; -2.