Объяснение:
1) разложим числитель и знаменатель на множители. Из числителя вынесем 8 как общий множитель, в знаменателе воспользуемся формулой сокращённого умножения a^2-b^2 = (a-b)(a+b). Тогда будет 8*(x+4)/((x-4)(x+4)) => 8/(x-4) учитывая что x≠-4
2) 1) 7a/(b-3) и b/((b-3)(b+3)) => 7a*(b+3)/((b-3)(b+3)) и b/((b-3)(b+3))
Под 2) 1/(х-3)^2 и 1/((х-3)(х+3)) => (х+3)/((х-3)^2)*(х+3)) и (х-3)/((х-3)^2)*(х+3))
Номер 3)
1) t^2/(3*(t-2)) + 4/(3*(2-t)) => t^2/(3*(t-2)) — 4/(3*(t-2)) => (t^2-4)/(3*(t-2)) => (t+2)/3 с учётом t≠-2
2) a^2/((a-8)(a+8)) - a/(a+8) => (a^2-a*(a-8))/((a-8)(a+8)) => 8a/((a-8)(a+8))
(во вложении, график параболы)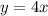
( во вложении, график прямой)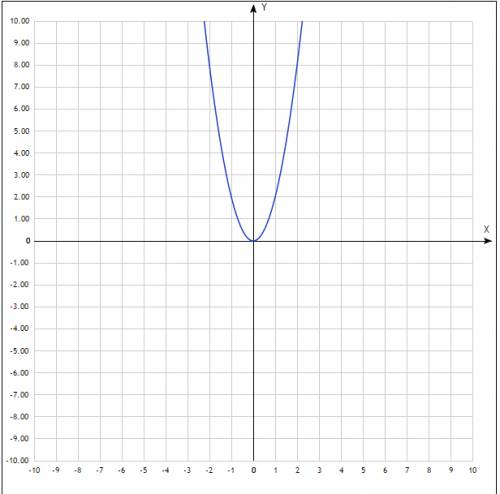
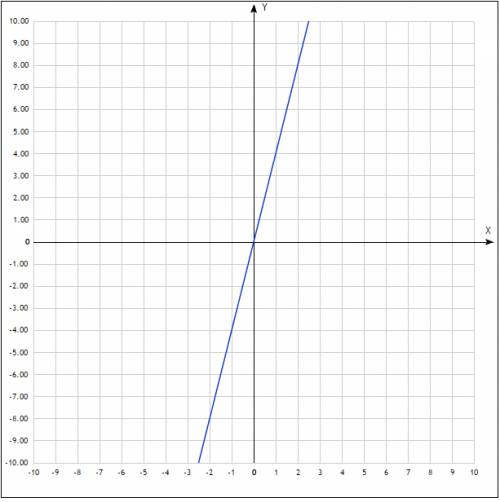
2) 64,2*(4/5)=51,36=5136/100 кг - в 1-ом ящике
3) Пусть во 2-ом ящике х кг.
тогда в 3-ем: 0.425*x
4) Составим уравнение:
51.36+x+0.425x=64.2
1.425x=64.2-51.36
1.425x=12.84
x=12.84/1.425=(1284/100):(1425/1000)=(1284*1000)/(100*1425)=1284*10/1425=1284*2/285=428*2/95=856/95 кг - во 2 ящике
5) 0,425*856/95=363,8/95=3638/950 кг - в 3 ящике.
ответ: 51.36, 856/95, 3638/950