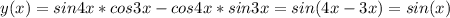
 есть
есть 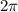
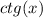 равен
равен 
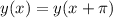
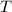 - искомый период, тогда
- искомый период, тогда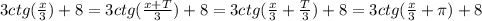
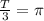

 относительно оси OX на 8 единиц вверх, также не влияя на период
относительно оси OX на 8 единиц вверх, также не влияя на период

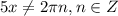
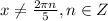
 - это симметричное относительно начала координат множество точек,
- это симметричное относительно начала координат множество точек, также симметрична относительно начала координат. Это означает, что есть смысл проверять функцию на парность, дальше.
также симметрична относительно начала координат. Это означает, что есть смысл проверять функцию на парность, дальше.
Объяснение:
1) А(-π/2 ; -1).
Здесь х= - π/2;
Для определения принадлежит ли точка А графику функции y=cos x
подставим значение х= - π/2, в формулу данной ф-ции:
y=cos x = cos (-π/2) =0. Итак при х= -π/2 , значение ф-ции у=0, а
это значит что точка А(-π/2;-1) не принадлежит графику функции
y=cos x.
2) B(9π/4; √2/2).
Объяснение аналогично варианту 1).
x= 9π/4;
Подставляем значения х в формулу данной функции:
y=cos x= cos(9π/4) = cos(2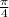 ) =cos(π/4 + 2π)= cos(π/4)= √2/2;
) =cos(π/4 + 2π)= cos(π/4)= √2/2;
При х =9π/4, значение функции у=√2/2, то точка В(9π/4; √2/2)
принадлежит графику функции y=cos x.
3) C(-4π;-1).
x=-4π; y=cos x= cos(-4π)=cos(-2π-2π)=cos(-2π)=cos(2π)=1;
При х= -4π, у=1.
Точка В(-4π;-1) не принадлежит графику функции y=cos x.
k∈Z
| sin x |≤1, значит k=-1 или k=1
sin x =1, x=π/2+2πn. n∈Z
sin x =-1, x= -π/2 + 2πm, m∈Z
2) π·cosx=πk, k∈Z
cosx=k, k∈Z
Функция у=cos x ограничена, | cos x |≤1
при k=-1 cos x =-1, x = π+2πn, n∈Z
при k=1 cos x=1, x = 2πm, m∈Z
при k=0 cos x=0, x = π/2+πl, l∈Z
3) В силу ограниченности функций косинус и синус:
-1≤cos2 x≤1
-2≤ 2cos 2x≤2 (1)
-1≤sin5x≤1
-1≤-sin5x≤1 (2)
Сложим (1) и (2)
-3≤2 cos 2x-sin5x≤3
Значит равенство -3 возможно лишь при
k,n∈Z
k,n∈Z
ответ. х=π/2+πk, k∈Z
4) cos²x+sin²x=1
Возведём обе части в квадрат:
cos⁴ х+ 2 cos²x sin²x + sin ⁴x=1,
cos⁴x+sin⁴x=1-2cos²xsin²x
Данное уравнение примет вид:
1-2 sin²x cos²x=|sinx cos x|
Введём новую переменную:
| sin x cos x |= t, t>0
1-2t²-t=0 или
2t²+t-1=0
D=b²-4ac=1-4·2(-1)=9=3²
t₁=(-1-3)/4=-1 (не удовлетворяет условию t>0) t₂=(-1+3)/4=1/2
|sinx cosx|=1/2 или | sin 2x |=1
а) sin2x=1
2x=π/2+2πk, k∈Z ⇒ x=π/4+πk, k∈Z
или
б) sin 2x =-1
2x=-π/2 +2πm, m∈Z ⇒ x=-π/4 +πm, m∈Z
ответ x=π/4+πk, x=-π/4 +πm, k, m ∈Z