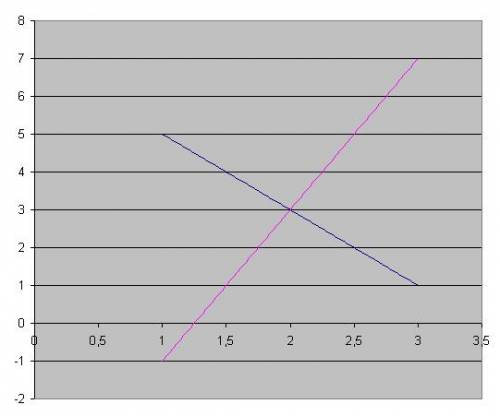
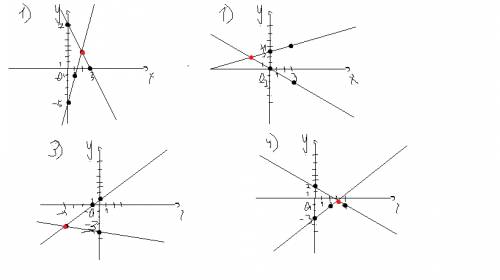
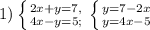 . Первый график построим по точкам (0; 7) и (7; 1), второй - (0; -5) и (-5; -1). Графики во вложении.
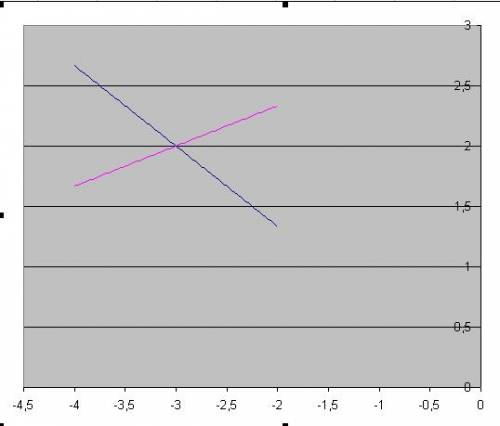
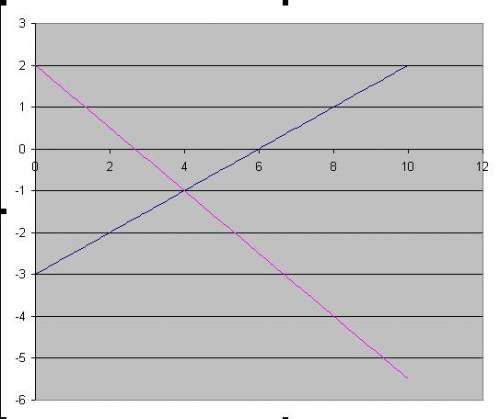
. Первый график построим по точкам (0; 7) и (7; 1), второй - (0; -5) и (-5; -1). Графики во вложении.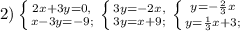 . Точки для первого - (0; 0), (0; -2), для второго - (0; 3) и (3; 4).
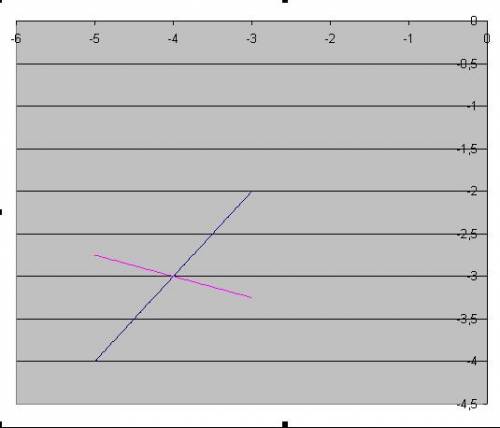
. Точки для первого - (0; 0), (0; -2), для второго - (0; 3) и (3; 4).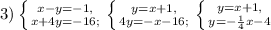 . Точки для первого - (0; 1) и (-1; 0), для второго - (0; -4) и (-4; -3).
. Точки для первого - (0; 1) и (-1; 0), для второго - (0; -4) и (-4; -3).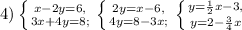
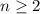 равных частей
равных частей
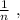 нужно разрезать верёвочку длины 2 на
нужно разрезать верёвочку длины 2 на  частей.
частей.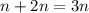 частей.
частей.