1.
a) (-3/4)²=(-0.75)²=0.5625
б) (-2)³+7 = -8+7 = -1
2.
8-(2x+3) = 7
8-2x-3=7
-2x=7-8+3
-2x=2
x= -1
3.
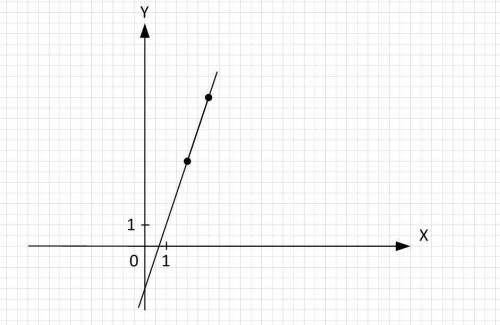
y=3x-2 линейная функция, графиком является прямая, для построения достаточно двух точек
x= 2 y=3*2-2=4
х = 3 у=3*3-2=7
график на приложенной картинке
4.
12x²y+3xy³ = 3xy(4x+y²)
5. a) 3v+5
6.
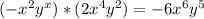
7.
(x-1)²+2x = x²-2x-1+2x=x²+1
8.
(1-3m)(2m+5)+6m(m-2) = 2m+5-6m²-16m+6m²-12m= 5-26m
9.
x+3y=7
3x+y=5
из первого уравнения:
x=7-3y
подставляем во второе
3(7-3y)+y=5
21-9y+y=5
-8y=-16
y=2
вычислим x:
x=7-3y = 7-3*2=1
х=1
y=2
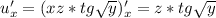
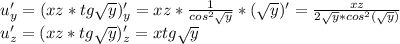
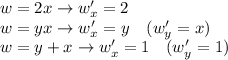
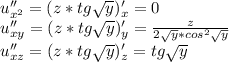
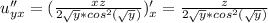
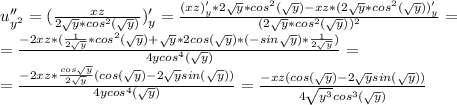
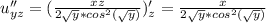
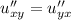
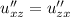
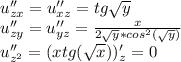
пусть
х²+6х=а
(а+4)*(а+6)=120
а²+4а+6а+24=120
а²+10а+24=120
а²+10а+24-120=0
а²+10а-96=0
Д=100-4*1(-96)=484=22²
а1=-10+22\2=6
а2=-10-22\2=-16
подстановка
1)х²+6х=а
а=6
х²+6х=6
х²+6х-6=0
Д=36-4*1*(-6)=60
х1=-6-√60\2
х2=-6+√60\2
2)х²+6х=а
а=-16
х²+6х=-16
х²+6х+16=0
Д=36-4*1*(-16)=100=10²
х1=-6-10\2=-16\2=-8
х2=-6+10\2=4\2=2
тогда действительные корни и их сумма будут
-8+(+2)=-6