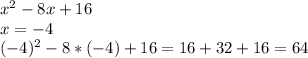
По свойству арифметической прогрессии:
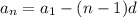
У нас известно 2 члена арифметической прогрессии, составим из них систему и найдем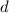 
и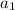 
:
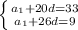
Выражаем ихз первого 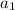и получаем:
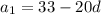
Подставляем во второе и получаем:
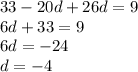
Подставляем d в выражение для 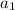и получаем:
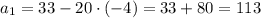
Теперь напишем формулу для суммы n членов арифметической прогрессии:
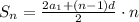
теперь подставляем в это выражение найденные числа и получаем:
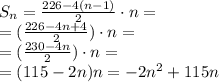
Получилась функция, которая зависит от n.
Нужно найти ее максимум:
Поскольку это парабола ветви которой направлены вниз (потому что перед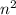 
стоит отрицательный коэффициент), то максимумом у нее будет точка, где производная принимает значение равное 0.
Найдем производную по n от этой функции:
Получим:
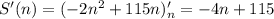
Теперь надо найти где она равно 0.
Решаем уравнение: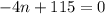 
получаем: 
Теперь осталось выяснить какое n нам взять. n=28 или n=29.
Для этого надо просто вычислить значение суммы при n=28 и при n=29
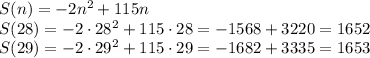
Как мы видим S(29)>S(28),
значит при n=29 сумма принимает максимальное значение равное 1653
ответ: максимальное значение суммы первых n членов арифметической прогрессии равно 1653 и достигается при n=29
при а=-4 имеем неравенство
-2*(-4)х+2*(-4)-6<0;
8x-8-6<0;
8x<14;
x<14/8;
при а=-4 неравенство выполняется не для всех действительных значений х.
Теперь пусть а не равно -4. Имеем квадратное неравество. Чтобы оно выполнялось для любого действительного х необходимо два условия
первое (коэфициент при x^2 должен быть меньше 0 - ветви параболы опущены вниз)
a+4<0; a<-4
второе (дискриминант исходного неравенства должен быть отрицательным - и тогда парабола лежит под осью абсцисс)
D<0
D=(-2a)^2-4(a+4)*(2a-6)=4a^2-8a^2-8a+96=-4a^2-8a^2+96
-4a^2-8a^2+96<0
a^2+2a-24>0
(a+6)(a-4)>0
a є (-бесконечность; -6)обьединение(4;+бесконечсть)
обьединяя получаем ответ: а є (-бесконечность; -6)
