Определим общее число расстановок на пяти позициях 5 шариков:
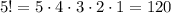
Однако, среди этих расстановок есть недопустимые (то есть те, при которых между зеленым и желтым шариком располагаются два или более шарика). Найдем число недопустимых расстановок.
Найдем число недопустимых размещений зеленого и желтого шарика. Их можно просто перечислить:
1) зеленый на 1-ом месте, желтый на 4-ом месте
2) зеленый на 1-ом месте, желтый на 5-ом месте
3) зеленый на 2-ом месте, желтый на 5-ом месте
4) зеленый на 4-ом месте, желтый на 1-ом месте
5) зеленый на 5-ом месте, желтый на 1-ом месте
6) зеленый на 5-ом месте, желтый на 1-ом месте
В каждом из этих случаев оставшиеся три шарика могут размещаться на свободных местах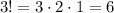 
Таким образом, всего имеется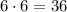 
недопустимых расстановок.
Значит, допустимых расстановок имеется:
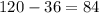
ответ: 84
В условии не сказано главного: каждое число встречается только один раз. То есть у Васи есть 22 карточки с числами от 1 до 22 и из них он должен составить пары. Поэтому максимум 10 пар. Больше просто не получится.
Первое, что на ум приходит, простые числа 17 и 19 не найдут себе пары. Их придется вычеркнуть.
У простого числа 11 единственная пара 22. Тогда простому числу 13 останется только 1. Оставшиеся 16 чисел пары себе находят.
Таким образом, поскольку 2 числа мы исключили (17 и 19), то число пар (22-2)/2=10
Графики функций
параллельны оси ОХ. Значит ось ОХ надо поднять или опустить на какое-то число. Если
Что касается второго задания.
Аргумент - это Х.
Функция - это Y.
Тебя спрашивают, чему будет равняться Y, если х=1,5 ты смотришь по графику и видишь 0. Так-же если тебя спросят, чему будет равнятся функция в аргументе 2, то по данному графику у тебя будет y=1.
Надеюсь, объяснил внятно.
Решения на фотографии. Удачи.