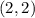
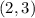
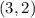
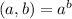 - где a-число оценок, b-число учеников.
- где a-число оценок, b-число учеников.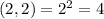
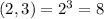
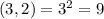
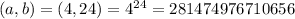
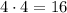 - варианта событий.
- варианта событий.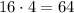 - варианта событий.
- варианта событий.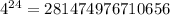 - вариантов событий.
- вариантов событий.
х² + х -30 ≤ 0
х² -х -20 ≥ 0
ищем корни квадратных трёхчленов:
х² + х -30 = 0 корни -6 и 5
х² -х -20 = 0 корни 5 и -4
-∞ [-6] [-4] [5] +∞
+ - - + знаки х² + х -30
+ + - + знаки х² -х -20
решение системы
ответ: х∈[-6; -4]
х+1-пропускная й трубы
420/х-2=399/(х+1)
420/х-2-399/(х+1)=0 домножим на х(х+1)
420(х+1)-2х(х+1)-399х=0
420х+420-2х²-2х-399х=0
-2х²+19х+420=0
2х²-19х-420=0
D = (-19)2 - 4·2·(-420) = 361 + 3360 = 3721
х₁=(19 - √3721)/(2*2)=(19-61)/4=-42/4=-10,5- не подходит
х₂=(19 + √3721)/(2*2)=(19+61)/4=80/4=20 л/мин- пропускная й трубы