В обеих точках функция непрерывна
Объяснение:
Для ответа на данный вопрос найдём пределы слева и справа от указанных точек, если пределы совпадают, то функция в данной точке непрерывна, если не совпадают, то функция имеет разрыв первого рода, а если хотя бы один из пределов равен бесконечности или не существует, то в данной точке функция имеет разрыв второго рода.
для x = 0
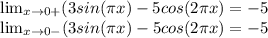
Как видим, пределы слева и справа совпадают, следовательно f(0) непрерывна
для x = 1
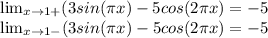
Снова видим, что пределы совпадают, следовательно и при f(1) функция непрерывна.
В решении.
Объяснение:
2. Чи належить графіку функції у = х² - х +1 точка:
1) А (0 ;-1)
2) В(0; 1)
3) С(2;0)
4) D(1;1)
5) Е(-2;6)
Чтобы определить принадлежность точки графику, нужно известные значения х и у (координаты точки) подставить в уравнение. Если левая часть равна правой, то принадлежит, и наоборот.
1) у = х² - х +1 А(0; -1)
-1 = 0² - 0 + 1
-1 ≠ 1, не принадлежит.
2) у = х² - х +1 В(0; 1)
1 = 0² - 0 + 1
1 = 1, принадлежит.
3) у = х² - х +1 С(2; 0)
0 = 2² - 2 + 1
0 ≠ 3, не принадлежит.
4) у = х² - х +1 D(1; 1)
1 = 1² - 1 + 1
1 = 1, принадлежит.
5) у = х² - х +1 Е(-2; 6)
6 = (-2)² -(-2) + 1
6 ≠ 7, не принадлежит.
Возводим обе части в квадрат
2х-5 + 2√(2х-5)·√(х+1)+х+1=х+6
2√(2х-5)·√(х+1)=х+6-2х+5-х-1
2√(2х-5)·√(х+1)=10-2x
Делим на 2
√(2х-5)·√(х+1)=5-x
Возводим в квадрат
(2х-5)(х+1) = 25-10х+х²,
2х²-5х+2х-5 = 25-10х+х²,
х² +7х -30 = 0
D=49+4·30=169=13²
х=(-7-13)/2=-10 или х=(-7+13)/2=3
Так как возводили в квадрат, то могли появиться посторонние корни, поэтому ОДЗ не находили, а теперь обязательно сделаем проверку.
при х=-10 √х+1 не существует, подкоренное выражение отрицательное
при х=3 √(2·3-5)+√(3+1)=√(3+9) - верно 1+2=3 - верно
ответ х=3