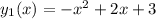 (1)
(1)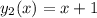 (2)
(2)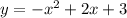 (1)
(1)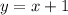 (2)
(2)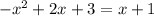
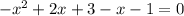
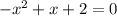 (3)
(3)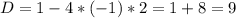
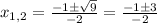
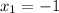
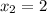
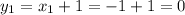
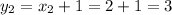
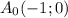

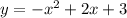 в параболу
в параболу  .
.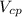 будет равен:
будет равен: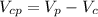 (4)
(4)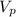 объем фигуры ограниченной, параболами и плоскостью перпендикулярной плоскости рисунка и проходящей через прямую
объем фигуры ограниченной, параболами и плоскостью перпендикулярной плоскости рисунка и проходящей через прямую 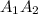 .
.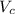 ? , объем конуса ограниченного прямыми и той же плоскостью проходящей через
? , объем конуса ограниченного прямыми и той же плоскостью проходящей через 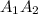
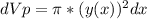
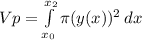 (5)
(5)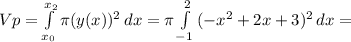
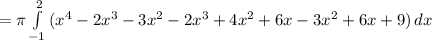
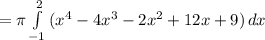 (6)
(6)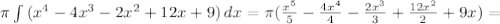
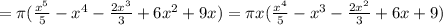 (7)
(7)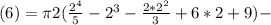
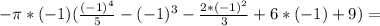
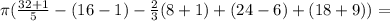
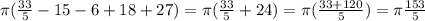 (8)
(8)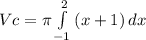 (9)
(9)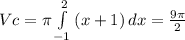 (10)
(10)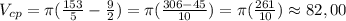
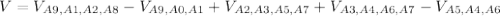
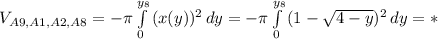
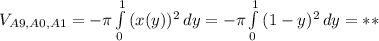

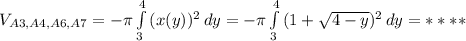

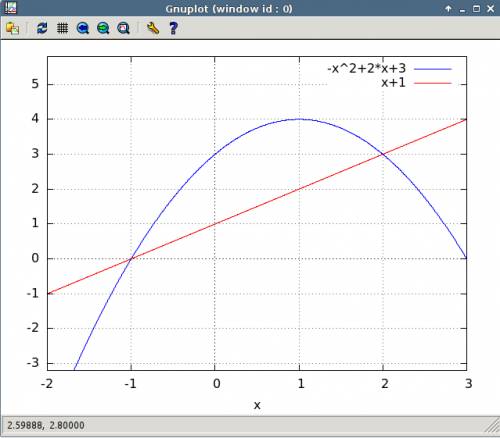
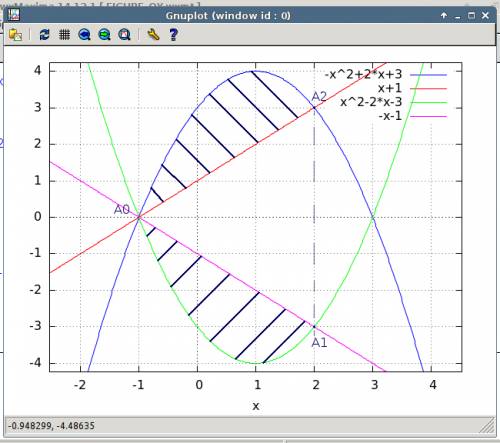
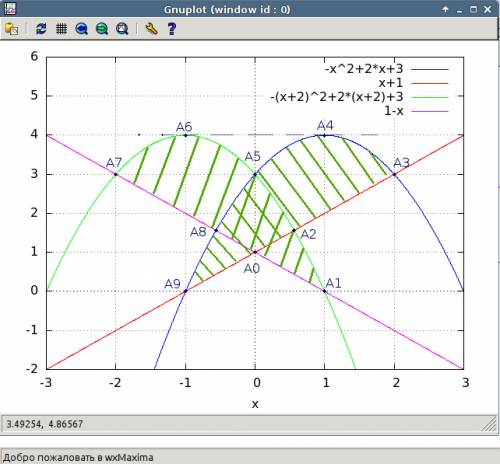
Перепишем функцию в виде уравнения.
y = − 3 x + 4
Воспользуемся уравнением для пучка прямых, проходящих через заданную точку для того, чтобы найти угловой коэффициент и точку пересечения с осью Y.
Угловой коэффициент: − 3
пересечение с осью Y: 4
Любую прямую можно построить при двух точек. Выберем два значения
x и подставим их в уравнение, чтобы определить соответствующие значения y .
x \y
0 \4
1 \1
Построим прямую с углового коэффициента и пересечения с осью Y или опираясь на две точки прямой.
Угловой коэффициент: − 3
пересечение с осью Y: 4
x\ y
0\ 4
1 \1
Объяснение:
x≠0
x≠-1
второй корень не удовл. ОДЗ