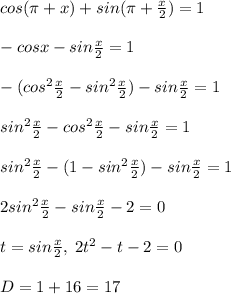
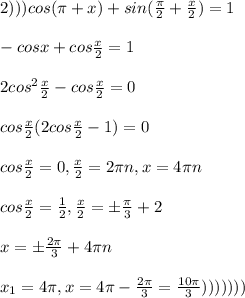
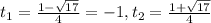
![sin\frac{x}{2}=\frac{1+\sqrt{17}}{4}1\; net\; resheniya\; (\sqrt{17}\approx 4,12)\\\\sin\frac{x}{2}=\frac{1-\sqrt{17}}{4},\frac{x}{2}=(-1)^{n}arcsin\frac{1-\sqrt{17}}{4}+\pi n,\; n\in Z\\\\x=2arcsin\frac{1-\sqrt{17}}{4}+2\pi n\\\\x=4\pi -arcsin\frac{1-\sqrt{17}}{4}\in (3\pi ;\frac{9\pi}{2}]](/tpl/images/0283/7601/508e7.png)
![x=3\pi +arcsin\frac{1-\sqrt{17}}{4}}\in (3\pi;\frac{9\pi}{2}]](/tpl/images/0283/7601/d57e7.png)
ответ во влажении!
################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################
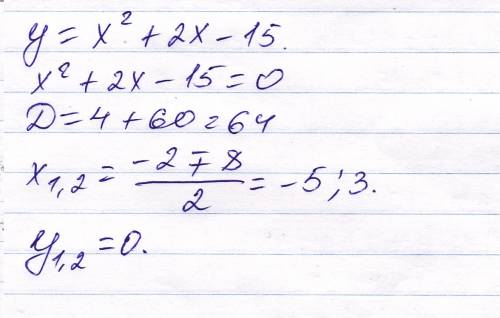
график ф-ии будет задан формулой y=(x+4)(x^2-4x+4)-22
y = x^3-4x^2+4x+4x^2-16x+16-22
y = x^3 - 12x - 6
несомненно, что это кубическая парабола, найдем ее точки перегиба
y' = 3x^2 - 12 = 0 решив это уравнение получаем, что точки перегиба в точках x=-2 и х=2
найдем значения ф-ии в точках перегиба и на концах отрезка
x=-4 y=-22
x=-2 y=10
x=2 y=-22
x=3 y=-15
максимальное значение ф-ии в точке х=-2 равное 10
ответ 10
но проще всего просто написать программку, которая перебирает значение с шагом в 1/1000 по всему заданному приоду и выводит максимум и минимум