Задача:
В двух кассах кинотеатра за два дня было продано всего 792 билета. Если в первой кассе было продано на 86 больше билетов, чем во второй, сколько билетов было продано в каждой кассе?
353 билетов продано во второй кассе и 439 в первой кассе
Объяснение:
1) Уравнение:
За х обозначим меньшую величину, т.е. :
х билетов в второй кассе, тогда:
х+86 билетов в первой кассе, т.к. в первой кассе было продано на 86 больше билетов, чем во второй, теперь:
х+х+86=792
2х+86=792
2х=792-86
2х=706
х=706:2
х=353
2) Теперь мы знаем, что во 2 кассе продано 353 билетов и узнаем сколько билетов продано в 1 кассе:
Вариант 1:
792-353=439
Вариант 2:
353+86=439
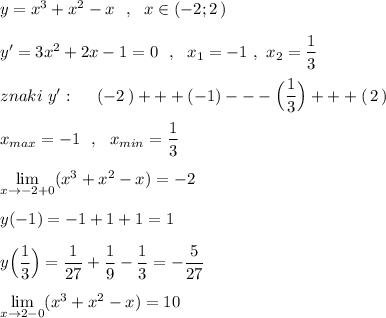
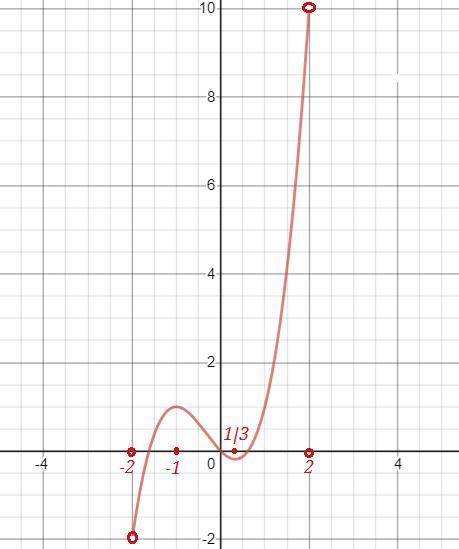
Так как значение функции в точке минимума на интервале (-2;2) больше, чем правосторонний предел функции в точке х= -2,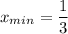 
и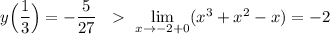 
, точка х= -2 не входит в исследуемый промежуток , то наименьшего значения функции найти нельзя. Значения функции ограничены снизу величиной (-2) .
Кстати, нельзя в этом случае найти и наибольшего значения функции на интервале (-2;2), так как
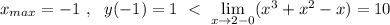. Значения функции ограничены сверху величиной 10 .
Смотри график.
Если по условию надо найти наименьшее значение функции на сегменте [-2;2 ] , то решение написано ниже.
![y=x^3+x^2-x\ \ ,\ \ x\in [-2;2\ ]\\\\y'=3x^2+2x-1=0\ \ ,\ \ x_1=-1\ ,\ x_2=\dfrac{1}{3}\\\\znaki\ y':\ \ \ \ [-2\, ]+++(-1)---\Big(\dfrac{1}{3}\Big )+++[\, 2\, ]\\\\y(-2)=-8+4+2=-2\\\\y(-1)=-1+1+1=1\\\\y\Big(\dfrac{1}{3}\Big)=\dfrac{1}{27}+\dfrac{1}{9}-\dfrac{1}{3}=-\dfrac{5}{27}\\\\y(2)=8+4-2=10\\\\y(naimen)=min\, y(x)_{[-2;2]}=-2=y(-2)](/tpl/images/1357/2432/cb39d.png)
x2=25
x=25:2
x=12.5