Объяснение:
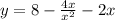
На 0 делить нельзя. Область определения: (-∞;0)∪(0;∞)
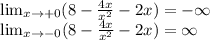
Т.к х не равен 0, то точек пересечения с осью у нет. Находим точки пересечения с осью х.
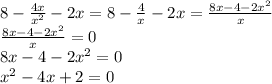
Решаем квадратное уравнение, находим точки пересечения с осью х:
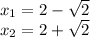
Находим точки экстремума (производная равна нулю).
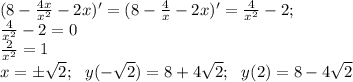
Для нахождения точек перегиба находим вторую производную
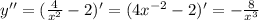
Вторая производная нигде не равна нулю, точек перегиба нет.
Горизонтальных асимптот нет. Вертикальная асимптота одна: х=0.
Ищем наклонную асимптоту:
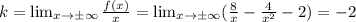
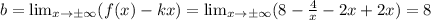
Наклонная асимптота есть:
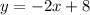
Дальнейшее исследование проводим, заполняя таблицу (см. рис.1).
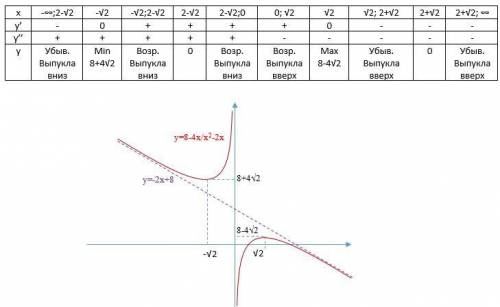
Итак. Нам нужно решить уравнение.
Решение таких уравнений основывается на простом факте. Вот он: если уравнение с целыми коэффициентами при неизвестных имеет ЦЕЛЫЙ корень, то искать его нужно среди делителей свободного члена.
Свободный член у нас равен 6. Надо перебрать все его делители. Кандидаты на ответ следующие: +-1;+-2;+-3;+-6. Иначе говоря, мы сейчас угадаем один их корней уравнения, по которому мы найдём позже все остальные. Просто подставляем все делители 6 в уравнение, проверяя, чтобы было равенство. Проверяем:
x = 1 1 - 1 - 3 - 2 + 2 + 6 = 3 - не 0, x = 1 - не корень уравнения
Аналогично проверьте все остальные случаи.