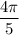Логарифмические функции с основанием 7 и 4 возрастающие, значит бо`льшему значению функции соответствует бо`льшее значение аргумента:
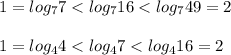
Числа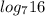 и
и 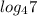 находятся на промежутке [1;2]
находятся на промежутке [1;2]
Сравним каждое c серединой этого отрезка, с числом 1,5
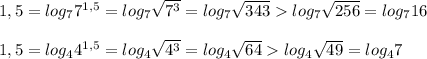
Значит оба числа находятся на промежутке [1;1,5]
Умножим равенства
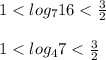
на 2.
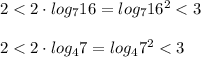
Числа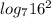 и
и 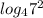 находятся на промежутке [2;3]
находятся на промежутке [2;3]
Сравним каждое c серединой этого отрезка, с числом 2,5
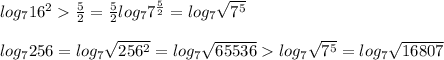
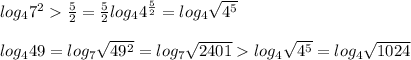
Числа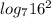 и
и 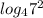 находятся на промежутке [2,5;3]
находятся на промежутке [2,5;3]
Умножим равенства

на 2.

Числа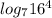 и
и 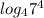 находятся на промежутке [5;6]
находятся на промежутке [5;6]
Сравним каждое c серединой этого отрезка, с числом 5,5
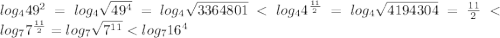
Получили:
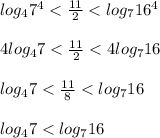
Дугу можно измерять угловой мерой (размер центрального угла, опирающего на дугу) или длиной (угловая мера умноженная на радиус). Числовая окружность имеет радиус 1, поэтому значение угловой меры численно равно значению длины.
Половина окружности это π и это же длина дуги (для числовой окружности).
∪AC = π = 2·∪AB ⇒ ∪AB =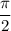
Пусть ∪AM = , тогда ∪MB =
, тогда ∪MB = 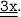
Т.к. первая четверть это ∪AB.
∪AM + ∪MB = 2x+3x = 5x =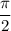 ⇒
⇒
x =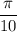 ⇒
⇒ 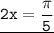 ;
; 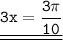
∪DM = ∪DA + ∪AM =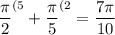
∪MC = ∪MB + ∪BC =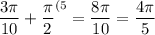
ответ: длина ∪AM =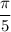
длина ∪MB =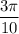
длина ∪DM =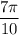
длина ∪MC =