15+3=18(км/ч) - скорость лодки по течению
15-3=12 (км/ч) - скорость лодки против течения
Пусть расстояние, на которое отплыли туристы, равно х км. Тогда по течению они плыли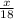 
часов, а против течения 
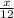часов. Учитывая привал, который длился 2 часа, всего в пути туристы были 16,25 - 8 - 2 = 6,25 (часов). Составляем уравнение:
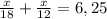
2х+3х=225
5х=225
х=45
ответ. 45 км.
1210
Объяснение:
Двухзначные числа, которые делятся на 4 с остатком 1 — это числа, которые делятся на 4 и ещё мы к ним добавляем 1 (13, 17, 21 и т.д.)
всего таких чисел 22. Самое первое число — 13, последнее — 97. И тут мы воспользуемся методом Гауса. Это метод, когда пары чисел с конца и с начала дают одно и тоже число. и тогда можно просто поделить на 2 количество чисел, посчитать количество пар и умножить их количество на сумму первого и последнего числа.
Вернёмся к задаче. Так как 97+13=110, а пар у нас 22:2=11, то достаточно умножить 110 на 11. Это будет 1210. Вот и ответ!
sin x + cos x = 1;
Возведем правую и левую часть выражения в квадрат, тогда получим:
(sin x + cos x) ^ 2 = 1 ^ 2;
sin ^ 2 x + 2 * sin x * cos x + сos ^ 2 x = 1;
(sin ^ 2 x + cos ^ 2 x) + 2 * sin x * cos x = 1;
Так как, по формуле тригонометрии sin ^ 2 x + cos ^ 2 x = 1 и 2 * sin x * cos x = sin (2 * x), тогда получим:
1 + 2 * sin x * cos = 1;
2 * sin x * cos x = 1 - 1;
2 * sin x * cos x = 0;
sin x * cos x = 0;
1) sin x = 0;
x = pi * n, где n принадлежит Z;
2) cos x = 0;
x = pi / 2 + pi * n, где n принадлежит Z.
Пусть х - искомое расстояние. Тогда до привала они плыли по течению -
- х/18 часов. Потом привал - 2 часа, потом обратно то же расстояние, но против течения - х/12 часов. Общее время: 16,25 - 8 = 8,25 часа.
Уравнение:
х/18 + 2 + х/12 = 8,25
Или х/18 + х/12 = 25/4
(5/36)*х = 225/36
х = 225/5 = 45 км.
ответ: 45 км.