cos x≠0. Поэтому обе части уравнения делим на √13 соs x.
tg x + tg² x = 0
tg x (1+tg x) = 0
tg x=0 1+tg x=0
x₁ = πn, n∈Z tg x=-1
x₂ = -π/4 + πn, n∈Z
1) Уравнение x²-(2a-4)x+(a²-25) имеет 1 корень при D = 0.
D = b²-4ac
D = (-(2a-4))²-4*1*(a²-25) = 4a²-16a+16-4a²+100
-16a+116 = 0
a = 116/16 = 29/4.
Чтобы было 2 корня, D должно быть больше 0,
т.е. а<29/4, таких значений бесконечное множество.
2) Уравнение x²-(2a-6)x+(a²-36) имеет не более 1, т.е.1 корень при D = 0, а менее , т.е. ни одного при D < 0.
D = b²-4ac
D = (-(2a-6))²-4*1*(a²-36) = 4a²-24a+36-4a²+144
-24a+180 = 0
a = 180/24 =15/2 - один корень,
при a >15/2
Объяснение:
Данные задачи решаются по одному алгоритму.
Продемонстрируем на примере первой функции (вторая исследуется аналогично, только функция не определена в точке х=4):
1)
Функция не определена в точке x = - 4.
Поэтому:
x ∈ (-∞; -4) ∪ (-4; +∞)
2)
Находим производную функции:
y'(x) = [(x²+3x)'·(x+4)-(x²+3x)·(x+4)'] / (x+4)²
y'(x) = [(2x+3)·(x+4)-(x²+3x)·1] / (x+4)²
y'(x) = (x²+8x+12) / (x+4)²
3)
Приравняем производную к нулю:
x²+8x+12 = 0
x₁ = - 6
x₂ = -2
4)
На интервале x∈(-∞; -6)
y'(x) > 0; функция монотонно возрастает.
На интервале x∈(-6; -4)
y'(x) < 0; функция монотонно убывает.
В точке x = -6 - максимум функции.
y(-6) = - 9
5)
На интервале x∈( -4; -2)
y'(x) < 0; функция монотонно убывает .
На интервале x∈(-2; +∞)
y'(x) > 0; функция монотонно возрастает.
В точке x = - 2 - минимум функции.
y(-2) = -1
6)
Для контроля строим график:
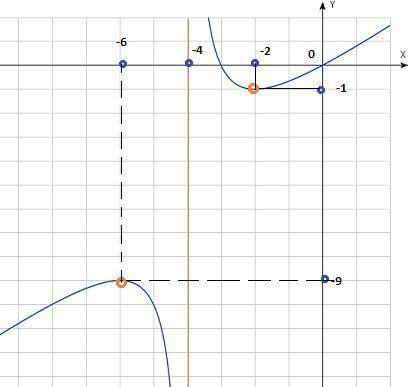2) [tex]y(x)=\frac{x^{2}" />
Вероятно 13cosx стоит под корнем.
Тогда ОДЗ: cosx больше 0
И ответы в задаче будут скорректированы с учетом ОДЗ:
х = 2Пк; (-П/4) + 2Пn k,n прин Z.