log₁₆x + log₁₆x² + log₁₆x⁴ = 7
log₁₆x·x²·x⁴ = 7
log₁₆x⁷ = 7
x⁷ = 16⁷
x=16
ответ. 16
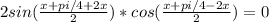
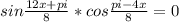
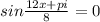
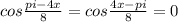
{9x+7y= 5. 11/63
{4x+3y = 2
║
∨
{9x+7y = 326/63;
{4x+3y = 2
Умножим обе части первого уравнения на 63 и получим cистему:
{567x+441y = 326;
{4x+3y = 2 |× (-147)
Умножим обе части второго уравнения на (-147) и получим систему:
{567x+441y = 326;
{-588x -441y = -294
Сложим эти уравнения и получим:
567х+441у-588х-441у=326-294
-21х = 32
х= - 32/21
Подставим х = - 32/21 во второе уравнение 4х + 3у = 2.
4*(-32/21)+3y = 2
3у= 2+128/21
3у = 42/21+128/21
3у =170/21
у = 170/63
Проверка
9*(-32/21) + 7 * 170/63=-864/63+1190/63=326/63=5 11/63
4*(-32/21) +3*(170/63) = -384/63+510/63= 2
Равенства верны.
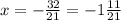
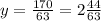
ответ: x=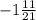 ; y=
; y=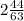
(1/4)log(2) x + (1/2)log(2) x + log(2) x = 7
log(2) x^(1/4 + 1/2 + 1) = 7
x^(7/4) = 2^7
x^(7/4) = 16 ^ (7/4)
x = 16