20 дней и 30 дней.
Объяснение:
Пусть один из сварщиков может выполнить всю работу за х дней,
тогда другой сварщик - за (25 * 2 - х) дней или (50 - х) дней.
Примем всю работу за 1, тогда производительность труда у первого сварщика равна 1/х, у второго сварщика - 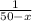 .
.
Совместна производительность труда двух сварщиков равна:
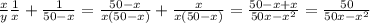
Составим уравнение и решим его:
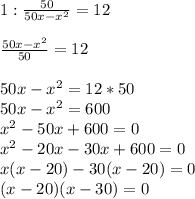
1) x - 20 = 0
x = 20 (дней)
2) x - 30 = 0
x = 30 (дней)
Допустим, что один из сварщиков может выполнить всю работу за 20 дней, тогда второй сварщик может выполнить всю работу за:
50 - 20 = 30 (дней) и наоборот.
{ x + y = 10
{ 1/x + 1/y = 5/12
Из условия понимаем, что ни х, ни у не равны 0, так как иначе не существовало бы обратных им чисел => можно домножить вторую часть системы на ху, чтобы избавиться от дробей:
у + х = 5ху/12
Но из первой части системы мы знаем, что х + у = 10. Получаем:
5ху/12 = 10
5ху = 120
ху = 24
Вывод: x = 24/y
Совместив с первой частью изначальной системы, получаем:
24/у + у = 10
Домножим на у:
24 + у^2 = 10у
у^2 - 10у + 24 = 0
По Виету получаем, что у є {4; 6}
Из xy = 24 получаем, что х є {6; 4}
То есть, выходит два ответа: (4; 6) и (6; 4), но поскольку нам неважен порядок чисел, количество ответов сокращается до одного, и этот ответ: 4 и 6.
2)120-48 = 72 (стр) - осталось прочитать
ответ: 72 страницы