y=|x-2|-|x+1|
Разобьём числовую ось на три промежутка точками х=-1 и х=2.
---------------------[-1 ]--------------[ 2 ] --------------------
1) -∞<x≤-1 : (x-2)<0 ⇒|x-2|=-x+2 , (x+1)<0 ⇒ |x+1|=-x-1 ,
y=|x-2|-|x+1|=-x-2-(-x-1)=3
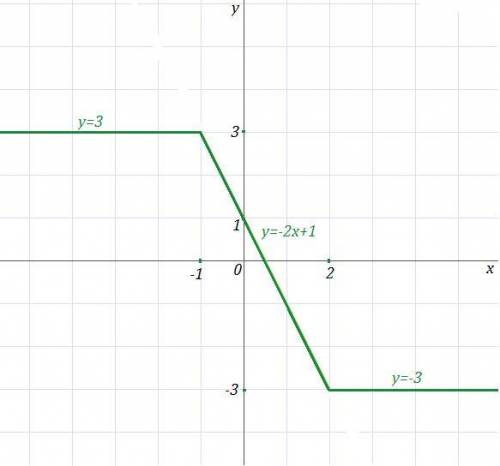
Строим на рассматриваемом промежутке прямую у=3 .
2) -1<x≤2 : (x-2)<0 ⇒ |x-2|=-x+2 , (x+1)>0 ⇒ |x+1|=x+1 ,
y=|x-2|-|x+1|=-x+2-(x+1)=-2x+1 .
Строим на промежутке (-1,2 ] прямую у= -2х+1 .
3) x>2 : (x+2)>0 ⇒ |x-2|=x-2 , (x+1)>0 ⇒ |x+1|=x+1 ,
y=|x-2|-|x+1|=x-2-(x+1)=-3 .
Строим при x>2 прямую у= -3 .
Доказательство от противного:
Предположим, дробь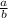 сократима. Это означает, что у чисел а и b есть общий простой множитель (назовем его k). Тогда число а можно представить в виде произведения mk, а число b - в виде произведения nk. Заменим а и b в дроби
сократима. Это означает, что у чисел а и b есть общий простой множитель (назовем его k). Тогда число а можно представить в виде произведения mk, а число b - в виде произведения nk. Заменим а и b в дроби 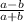 на эти выражения, получим:
на эти выражения, получим:
Вынесем k за скобки:
Числитель и знаменатель этой дроби можно сократить на k, но это противоречит условию, в котором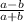 - несократимая дробь. Значит, наше предположение о том, что дробь
- несократимая дробь. Значит, наше предположение о том, что дробь 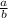 сократима - неверно, т.е эта дробь является несократимой (что и требовалось доказать)
сократима - неверно, т.е эта дробь является несократимой (что и требовалось доказать)