
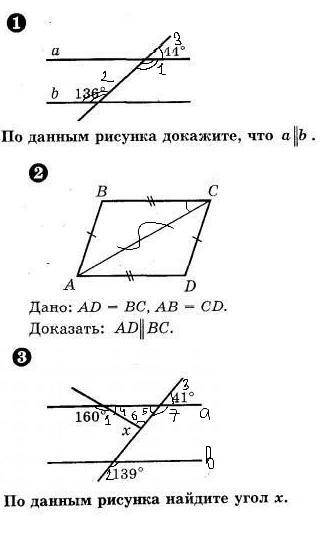
1. ∠1 и ∠3 смежные, значит ∠1 = 180° - ∠3 = 180° - 44° = 136°
∠1 и∠2 внутр. накрест лежащие углы, они равны между собой по 136° => a параллельно b
2. рассмотрим ΔABC и ΔADC.
они равны по 3 признаку, так как AC общая сторона, AD = BC и AB = CD
∠BCA = ∠DAC (как внутр. накрест лежащие углы), а из этого следует, что AD параллельно BC
3. обозначим на рисунке ∠4, ∠5, ∠6 и ∠7
∠7 = 180° - ∠3 = 180° - 41° = 139°, следовательно ∠7 = ∠3, значит a параллельно b
∠5 = ∠3 = 41° (как вертикальные)
∠4 = 180° - ∠1 = 180° - 160° = 20°
и ∠6 = 180° - ∠4 - ∠5 = 180° - 20° - 41° = 119°
следовательно угол, обозначенный как x, равен 180° - ∠6 = 180° - 119° = 61°
sinx > √2/2;
1. В первой четверти значение √2/2 синус принимает при x = π/4 = 45°, а во второй четверти - в точке x = 3π/4 = 135°.
2. На промежутке [π/4; π/2] функция возрастает от √2/2 до 1, а на промежутке [π/2; 3π/4] - убывает от 1 до значения √2/2. Следовательно, на интервале
(π/4; 3π/4) значение синусa больше √2/2;
sinx > √2/2;
x ∈ (π/4, 3π/4).
3. Поскольку синус периодическая функция с периодом 2π, то полное решение уравнения будет бесконечное множество промежутков:
x ∈ (π/4 + 2πk, 3π/4 + 2πk), k ∈ Z.
ответ: (π/4 + 2πk, 3π/4 + 2πk),
k ∈ Z.