task/30199707 решить неравенства:
1. 5²ˣ - 2²ˣ - 5²ˣ⁻¹- 2²ˣ⁺² ≥ 0 ⇔ 5²ˣ⁻¹(5-1) -2²ˣ(1+2²) ≥ 0 ⇔4*5²ˣ⁻¹ ≥ 5* 2²ˣ ⇔ 2²*5²ˣ⁻¹ ≥ 5*2²ˣ || : 5*2² || ⇔ 5²ˣ⁻² ≥ 2²ˣ⁻² ⇔ (5/2)²ˣ⁻² ≥ 1 ⇔
(5/2)²ˣ⁻² ≥ (5/2)⁰ , т.к. 5/2 > 1 ,то ⇔ 2x -2 ≥ 0 ⇔ x ≥ 1
ответ : x ∈ [ 1 ; +∞) .
2. √7²ˣ⁺⁶-√49ˣ⁺²-2ˣ⁺⁵+2*2²⁺ˣ > 0 ⇔(√7²)ˣ⁺³-(√7²)ˣ⁺²-2ˣ⁺²⁺³ +2*2ˣ⁺² >0 ⇔
7ˣ⁺³ -7ˣ⁺² - 2ˣ⁺²⁺³ +2*2ˣ⁺² >0 ⇔ 7ˣ⁺²(7 -1) -2ˣ⁺²(2³ -2) > 0 ⇔
6* 7ˣ⁺²> (8 -2)*2ˣ⁺³ || :6 || ⇔7ˣ⁺² >2ˣ⁺²⇔(7/2)ˣ⁺² > 1⇔(7/2)ˣ⁺² > (7/2)⁰ ⇔
x+2 > 0 ⇔ x > -2. ответ : x ∈ ( -2 ; +∞) .
Многочлен в левой части можно разложить на множители:
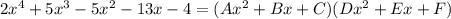 , где A, ..., F - некоторые целые коэффициенты. Раскроем скобки в правой части:
, где A, ..., F - некоторые целые коэффициенты. Раскроем скобки в правой части:
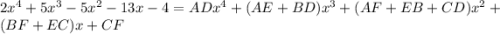
Многочлены равны, когда равны коэффициенты при соотвествующих степенях x. Составим систему уравнений (знак системы не пишу):
AD=2
AE+BD=5
AF+EB+CD=-5
BF+EC=-13
CF=-4
6 неизвестных и всего 5 уравнений - не айс. Но нас то, что A, ..., F - целые числа.
Взглянем на первое и последнее уравнение. Имеем 4 различных варианта значений A, D, C, F. Начинаем рассматривать, по порядку, когда найдем хотя бы одно решение системы, то все будет круто и дальше можно будет не продолжать:
A=1, D=2, C=1, F=-4:
E+2B=5
EB=-3
-4B+E=-13
Не забываем о том, что коэффициенты целые и быстро заключаем, что решением являются числа B=3, E=-1. Вот так повезло, с первого раза нашли подходящую систему. Итак
A=1, B=3, C=1, D=2, E=-1, F=-4
Тогда
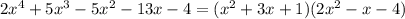
Уравнение принимает вид:
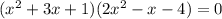
Дальше решит даже первоклассник
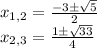
-1,5x=9
x=9 : (-1,5)
x=6
г) 12x - 1 = 35
12x=35+1
12x=36
x=36:12
x=3
д) -х + 4 = 47
-x=47-4
-x=43
x= - 43
е) 1,3х = 54 + х
1,3x-x=54
0,3x=54
x=54: 0,3
x=180
ж) 7 = 6 - 0,2х
0,2x=6-7
0,2x=1
x=1: 0,2
x=5
з) 0,15х + 6 = 51
0,15 x=51-6
0,15x=45
x=45:0,15
x=300
и) -0,7 + 2 = 65 (где тут переменная?)