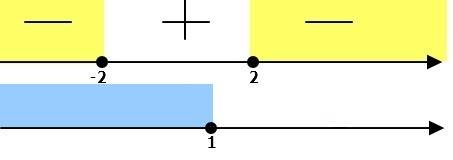
![\sqrt{5-2x} \leq 1-x\\ ===========\\ \left \{ {{5-2x \geq 0} \atop {1-x \geq 0}} \right. \\ \left \{ {{-2x \geq -5} \atop {-x \geq -1}} \right. \\ \left \{ {{x \leq 2.5} \atop {x \leq 1}} \right. \\ x\in (-\infty;1] \\ ===========\\ ( \sqrt{5-2x})^2 \leq (1-x)^2\\ 5-2x \leq 1-2x+x^2\\ 5-2x-1+2x-x^2 \leq 0\\ 4-x^2 \leq 0\\ (2-x)(2+x) \leq 0\\\\ \left \{ {{(2-x)(2+x) \leq 0} \atop {x \leq 1}} \right. \\\\ x\in (-\infty;-2]](/tpl/images/0084/5177/9c2f1.png)
Не очень понятно
Если под корнем (х-3), то
x-2-√(х-3)=0
х-2=√(х-3)
Возводим в квадрат обе части уравнения:
(х-2)²=(√(х-3))²
х²-4х+4=х-3
х²-5х+7=0
Найдем дискриминант квадратного уравнения:
D = b² - 4ac = (-5)² - 4·1·7 = 25 - 28 = -3
Так как дискриминант меньше нуля, то уравнение не имеет действительных решений.
Если под корнем х, то
x-2-√x-3=0
х-5=√х
Возводим в квадрат обе части уравнения:
(х-5)²=(√х)²
х²-10х+25=х
х²-11х+25=0
Найдем дискриминант квадратного уравнения:
D = b² - 4ac = (-11)² - 4·1·25 = 121 - 100 = 21
Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:
x1 = ≈ 3.2087
x2 = ≈ 7.7913
Как-то так, удачи))