а)2sin²x-3sinx-2=0
Замена sinx=t
2t²-3t-2=0
D=3²+4×2×2=25
t₁= 3+√D÷4=3+5÷ 4=8÷4=2
t₂=3-√D÷4=3-5÷4=-2÷4=-0,5
Возвращаемся к замене
sinx=2 sinx=-0,5
решения нет х=(1)⁻k(cтепень)arcsin(-1\2)+πn,n∈Z
-1≤sinx ≥1 x=(1)⁻k × -π\6 +πn,n∈Z
4cos²x+4sinx-1=0
cos²x=1-sin²x
4( 1-sin²x)+4sinx-1=0
4-4sin²x+4sinx-1=0
-4sin²x+4sinx-1+4=0
-4 sin²x+4sinx+3=0 ÷(-1)
4sin²x-4sinx-3=0
Замена sinx=t
4t²-4t-3=0
D=4²+4×4×3=16+48=64
t₁=4+√D÷8= 4+8÷8=12÷8=1,5
t₂=4-√D÷8=4-8÷8= -4÷8=-0,5
Возвращаемся к замене
sinx=1,5 sinx=-1\2
решения нет х=(1)⁻k(cтепень)arcsin(-1\2)+πn,n∈Z
-1≤sinx ≥1 x=(1)⁻k × -π\6 +πn,n∈Z
sin (5πx/9) = sin (πx/9) + sin (2πx/9)
sin (5πx/9) - sin (πx/9) = sin (2πx/9)
По формуле разности синусов:
2sin(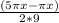
)cos(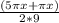
) - sin (2πx/9) = 0;
2 sin(2πx/9)cos(πx/3) - sin(2πx/9)=0;
sin (2πx/9) (2cos(πx/3)-1)=0;
sin (2πx/9)=0 или 2cos (πx/3)=1; cos (πx/3)=1/2
2πx/9=πn, n∈Z или πx/3=π/3+2πn, n∈Z или πx/3=-π/3+2πn, n∈Z;
Сокращаем на π:
2x/9=n, n∈Z или x/3=1/3+2n, n∈Z или x/3=-1/3+2n, n∈Z;
x=9n/2 или x=6n+1 или x=6n-1
Теперь отбираем корни уравнения, принадлежащие промежутку (4;8)
4<(9/2)n<8; 8/9<n<16/9; n=1, x=4,5
4<6n+1<8; 3<6n<7; 1/2<n<7/6; n=1; x=6+1=7;
4<6n-1<8; 5<6n<9; 5/6<n<3/2; n=1; x=6-1=5
ответ: x={4,5;5;7}
