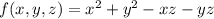
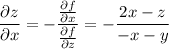
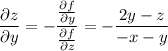
 с координатами
с координатами 
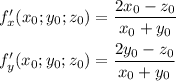
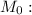
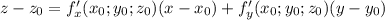 - уравнение касательной в общем виде.
- уравнение касательной в общем виде.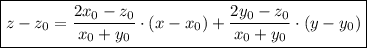 - уравнение касательной плоскости к поверхности в точке
- уравнение касательной плоскости к поверхности в точке  с координатами
с координатами 
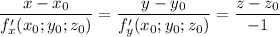
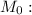
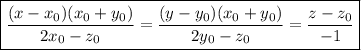 - каноническое уравнение нормали к поверхности в точке
- каноническое уравнение нормали к поверхности в точке  с координатами
с координатами 
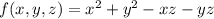
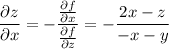
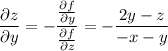
 с координатами
с координатами 
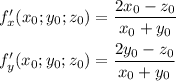
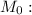
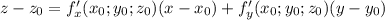 - уравнение касательной в общем виде.
- уравнение касательной в общем виде.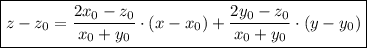 - уравнение касательной плоскости к поверхности в точке
- уравнение касательной плоскости к поверхности в точке  с координатами
с координатами 
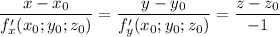
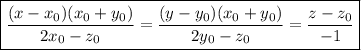 - каноническое уравнение нормали к поверхности в точке
- каноническое уравнение нормали к поверхности в точке  с координатами
с координатами 
Наименьшее значение в вершине параболы.
Выделим полный квадрат
х²-8х+7=х²-2х·4+16-16+7=(х²-8х+16)-9=(х-4)²-9
При х = 4 наименьшее значение (-9)
Координаты вершины параболы (4;-9)