найдем точки пересечения
x^2 - 4x + 3 = 8
x^2 - 4x -5=0
х= -1 х = 5
x^2 - 12x + 35 = 8
x^2 - 12x + 27=0
х = 3 х= 9
x^2 - 4x + 3 =x^2 - 12x + 35
8х = 32
х = 4
1) интеграл от 4 до 5 (8-(x^2 - 4x + 3 ))= 8х -x^3 /3 +2x^2 -3x = 25 -125/3 +50 - 32 +64/3 -32 =11 61/3 = 31 1/3
2) интеграл от3 до 4 (8-(x^2 - 12x + 35)) = 8х - x ^3 /3 +6x^2 -35x = -27*4 -64/3 +96 +27*3 +9 -54 = 24 -21 1/3 =2 2/3
31 1/3 +3 2/3 = 35
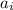- сторона i-ого треугольника
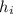- высота i-ого треугольника
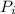- периметр i-ого треугольника
, значит если стороны заданных треугольников образую геометрическую прогрессию, то и их периметры также образуют геометрическую прогрессию.
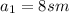. Так как треугольник равносторонний, то все его высоты равны. Найдем длину одной из них. Высота является противолежащим катетом для угла равностороннего треугольника 60 градусов, гипотенузой в таком прямоугольном треугольнике является сторона равностороннего треугольника: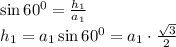
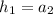, то: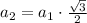
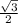(для геометрической прогрессии он и будет являться знаменателем).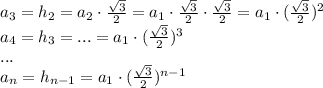
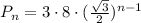
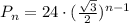- общая формула n-ого члена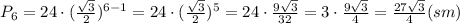
f '(x) = (3lnx² + cos(sinx) - √(x- 1))' = 6x/x² - sin(sinx)·cosx - 1/(2√(x- 1)) = 6/x - sin(sinx)·cosx - 1/(2√(x- 1))