1)arcsin 0 =0
2)arccos 1= 0 ;
3)arcsin√2/2 =π/4 ;
4)arccos 3 не существует угол косинус которой =3 ;
5)arcsin (-1) = -π/2 ;
6)arccos(-√3/2) = π -π/6 = 5π/6 ;
7)arctg 0 = 0 ;
8)arctg 1 =π/4 ;
9)arctg(-√3) = - π/3 ;
10)arcctg(-√3/3) = π -π/3= 2π/3 ;
11)arcsin(-1/2)+arccos 1 = -π/6 +0 = -π/6 ;
12) (arcsin -1)/2+ arccos 1 = -π/4+0= -π/4;
13)cos ( arccos 1) =1;
14)sin(arcsin√2/2) =√2/2 ;
15)arcsin (sin π/4) =arcsin(√2/2) =π/4 ;
16)arccos ( cos(-π/4))=arccos ( cos(π/4))=arccos (√2/2))=π/4 ;
17)cos (arcsin(-1/3))=cos(arccos(√8/3)= √8/3 =2√2/3 ;
18)tg(arccos(-1/4)) =tq(arctq(-√15) = - √15; 1+tq²α= 1/cos²α
19)sin(arcctg(-2)) =sin(arcsin(1/√5)=1/√5 ;
20) arcsin(cos π/9) =arcsin(sin(π/2 - π/9))=arcsin(sin7π/18) =7π/18 .
Подробнее - на -
Объяснение:
1. ОТВЕТ: например,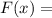 
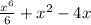, поскольку 
.
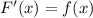Общий вид первообразных -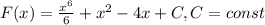 
2. Докажем, что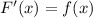 
:
.
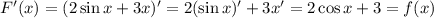Что и требовалось доказать.
3. Общий вид первообразных функции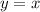 
- 
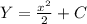, где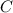 
- некоторое постоянное число. Если график первообразной проходит через точку 
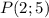, то это значит, что при подстановке 
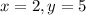получим верное равенство:
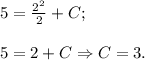
Искомая первообразная -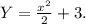 
ОТВЕТ: Y = x²/2 + 3.
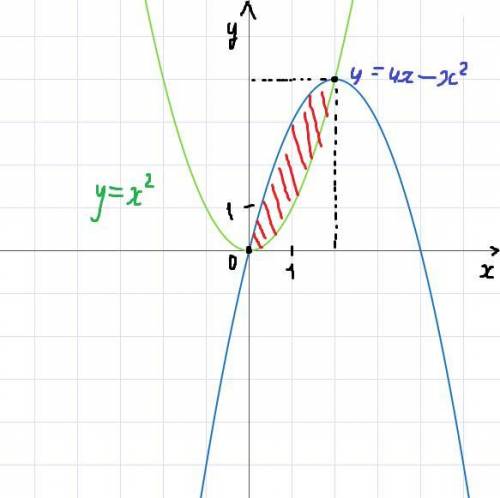
4. Графики функции - во вложении 1. Площадь заданной фигуры заштрихована красным.
Поскольку график функции y = 4x - x² на отрезке [0; 2] располагается как минимум не ниже графика функции y = x² (выполняется неравенство 4x - x² ≥ x²), то площадь будет иметь вид
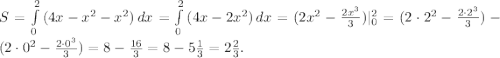
ОТВЕТ: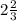 
кв. ед.
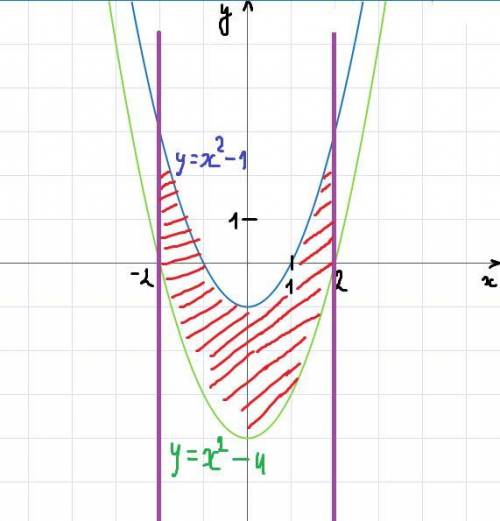
5. Графики - во вложении 2. Площадь заданной фигуры заштрихована красным.
Поскольку на отрезке (-2; 2) график функции y = x² - 1 располагается выше графика функции y = x² - 4 (выполняется равенство x² - 1 > x² - 4), то площадь будет иметь вид
![S=|\int\limits^2_{-2} {[x^2-1-(x^2-4)]} \, dx |=\int\limits^2_{-2} {3} \, dx= (3x)|_{-2}^2=3\cdot2-[3\cdot(-2)]=6+6=12](/tpl/images/1179/2526/6e4c7.png)
ОТВЕТ: 12 кв. ед.
6. Объем выполненной работы A(t) с момента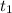 
по момент 
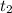согласно механическому смыслу определенного интеграла есть значение выражения интеграла
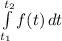
Имеем:
ОТВЕТ: ≈ 760.
4X + 5 = 6 + 5X - 15
4X + 5 = 5X - 9
5X - 4X = 5 + 9
X = 14