Пусть C — первая деталь окажется стандартной. Гипотезы:
H₁ - деталь изготовлена первым заводом;
H₂ - деталь изготовлена вторым заводом;
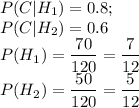
Вероятность события А по формуле полной вероятности
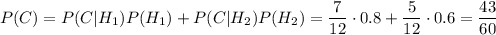
По формуле Байеса, вероятность того, что эта деталь изготовлена первым заводом, равна:
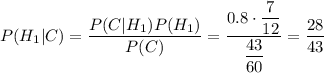
Аналогично, пусть В — вторая деталь окажется стандартной. Так как одна деталь уже вынута, то в партии остается 119 лампочек, из них 69 изготовлены на первом заводе.
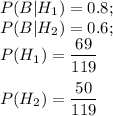
По формуле полной вероятности, вероятность события В:
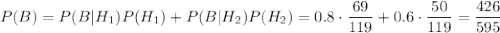
По формуле Байеса, вероятность того, что эта деталь изготовлена первым заводом, равна:
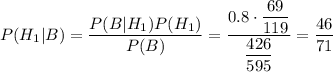
По теореме умножения, вероятность того, что наудачу взятые две лампочки являются стандартными, равна
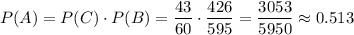
По теореме умножения, вероятность того, что обе лампочки изготовлены на первом заводе, при условии что событие А произошло, равна:
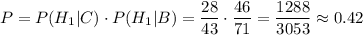
При делении целых чисел на 11 мы получаем остатки от 0 до 10. Рассмотрим какие остатки могут давать целые числа в пятой степени при делении на 11. Для этого достаточно возвести числа от 0 до 10 в пятую степень и рассмотреть остатки от их деления на 11. В итоге получим, что при делении целых чисел в пятой степени на 11 получаются остатки 0, 1 и 10. В левой части уравнения стоит сумма трех целых чисел в пятой степени. Следовательно, она может давать остатки 0, 1, 2, 3, 8, 9 и 10. Но 2009 при делении на 11 дает остаток 7. Следовательно уравнение не имеет решений в целых числах.
cos^2t=1-16/25=9/25⇒cost=3/5
tg t=sint/cost=
ctgt=cost/sint=3/4