Пусть m — произвольное значение
функции y. Тогда равенство y=m окажется верным при
тех значениях m, при которых уравнение y=f(x) относительно х
имеет корни. Найдем множество значений m, при которых эти уравнения имеют корни. Тем самым мы найдем область значений функций у.
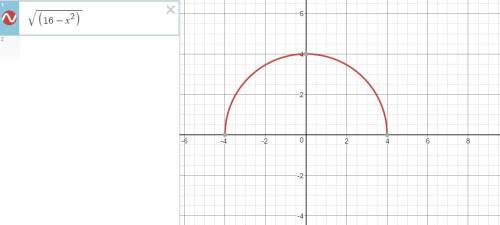
Возведем обе части уравнения √(16-x²)=m в квадрат и выразим x через m
1) m≥0;16-x²≥0⇒|x|≤4
16-x²=m²⇒x²-(16-m²)=0⇒|x|=√(16-m²)⇒√(16-m²)≤4⇒
|m|≤4;16-m²≤16⇒|m|≤4;m²≥0⇒m∈[0;4]
E(y)=[0;4] функция ограниченная
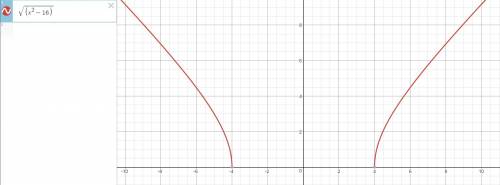
2) m≥0; x²-16≥0⇒|x|≥4
√(x²-16)=m⇒x²-16=m²⇒x²=m²+16⇒|x|=√(m²+16)⇒√(m²+16)≥4⇒
m²+16≥16⇒m²≥0⇒m≥0
E(y)=[0;∞) функция неограниченная
-4 < 9a + 5/6 < 3
-4 < 9а + 5/6;
9а + 5/6 < 3;
-4 - 9а - 5/6 < 0;
9а + 5/6 - 3 < 0;
-24 - 54а - 5 < 0;
54a + 5 - 18 < 0;
-54а - 29 < 0;
54а - 13 < 0;
-54а < 29;
54а < 13;
54а > -29;
54а < 13;
а > -29/54;
а < 13/54…
Если я, конечно, вычислила правильно, то Вам остаётся только провести координатную прямую, обозначить точки (это строгое неравенство, так что не ошибитесь), а дальше Вы знаете. К сожалению, я не уверена в правильности, очень странные числа, хоть и всё сто раз проверила. Но всё может быть)