В решении.
Объяснение:
Решить данные неравенства : (x+4)^2<0 x^2+4<0 x^2+3x<0;
1) (x + 4)² < 0
х² + 8х + 16 < 0
Приравнять к нулю и решить квадратное уравнение:
х² + 8х + 16 = 0
D=b²-4ac = 64 - 64 = 0 √D=0
х=(-b±√D)/2a
х=(-8±0)/2
х = -4.
Уравнение квадратичной функции, график - парабола. Значение х = -4 указывает на то, что парабола "стоит" на оси Ох в точке х= -4, весь график выше оси Ох, значит, у < 0 не существует.
Неравенство не имеет решения.
2) x² + 4 < 0
Приравнять к нулю и решить квадратное уравнение:
x² = -4
Уравнение не имеет действительных корней.
Неравенство не имеет решения.
3) x² + 3x < 0
Приравнять к нулю и решить неполное квадратное уравнение:
x² + 3x = 0
х(х + 3) = 0
х₁ = 0;
х + 3 = 0
х₂ = -3;
Уравнение квадратичной функции, график парабола, ветви направлены вверх, пересекают ось Ох в точках х= 0 и х= -3.
На промежутке от х= -3 до х=0 у<0 (парабола ниже оси Ох).
Решения неравенства: х∈(-3; 0).
Неравенство строгое, скобки круглые.
В решении.
Объяснение:
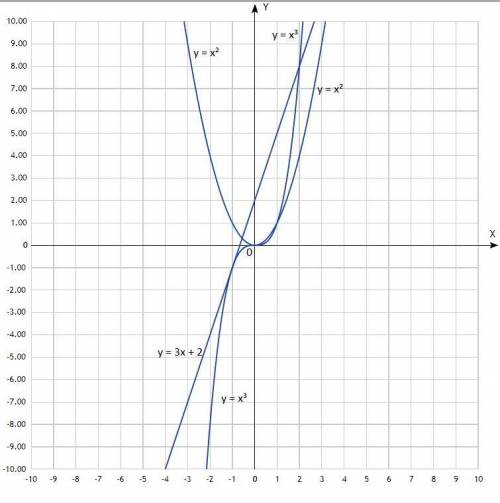
1) В одной и той же системе координат постройте графики
функций y = x^2, y = x^3 и y = 3x + 2.
а) у = х²;
График - классическая парабола с центром в начале координат, ветви направлены вверх.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
Таблица:
х -3 -2 -1 0 1 2 3
у 9 4 1 0 1 4 9
По вычисленным точкам построить параболу.
б) у = х³;
График - кубическая парабола с центром в начале координат.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
Таблица:
х -2 -1 0 1 2
у -8 -1 0 1 8
По вычисленным точкам построить параболу.
в) у = 3х + 2;
График линейной функции прямая линия.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу. Для построения прямой достаточно двух точек, для точности построения определить три.
Таблица:
х -1 0 1
у -1 2 5
По вычисленным точкам построить прямую.
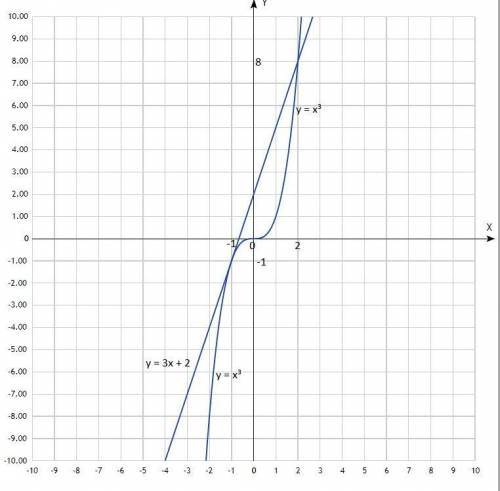
2) Решите графически уравнение x^3 = 3x + 2.
у = х³; у = 3х + 2;
Построить графики функций и найти координаты точек их пересечения.
а) у = х³;
График - кубическая парабола с центром в начале координат.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
Таблица:
х -2 -1 0 1 2
у -8 -1 0 1 8
По вычисленным точкам построить параболу.
б) у = 3х + 2;
График линейной функции прямая линия.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу. Для построения прямой достаточно двух точек, для точности построения определить три.
Таблица:
х -1 0 1
у -1 2 5
По вычисленным точкам построить прямую.
Координаты точек пересечения: (-1; -1); (2; 8).
Решения уравнения: х = -1; х = 2.
рассмотри по скобкам,если раскрыть скобки то увидим что х в кубической степени,а это значит данное уравнение имеет три корня
а)2х+3=0
2х=-3
х=-3\2=-1,5
б)3х-1=0
3х=1
х=1\3
в)х+2=0
х=-2
ответ(х1=-2,х2=1\3,х3=-1,5)
2)(x+4)(1+2x)(1-3x)=0
рассмотри по скобкам,если раскрыть скобки то увидим что х в кубической степени,а это значит данное уравнение имеет три корня
а)х+4=0
х=-4
б)2х+1=0
2х=-1
х=-1\2=-0,5
в)1-3х=0
-3х=-1
х=-1\(-3)=1\3
ответ (х1=-4,х2=-0,5, х3=1\3)