В 3 вопросе задания "Является ли число 7 членом арифметческой прогрессии?" не ясно, к какой прогрессии его отнести, поэтому проверяю для 1 и 2 прогрессий.
Дано: a₁=4, d=3
Найти: 1) а₁₃=?
2) является ли число 7 членом арифметической прогрессии?
a₁₃=a₁+d(n-1)
a₁₃=4+3(13-1)
a₁₃=40
a(n)=7 ?
7=4+3(n-1)
3n=6
n=2 - число 7 является вторым членом арифметической прогрессии.
Дана арифметическая прогрессия: -98; -96
Найти: 1) а₂₂=?
2) является ли число 7 членом арифметической прогрессии?
a₁=-98; a₂=-96
d=a₂-a₁
d=-96-(-98)=2
a₂₂=a₁+d(22-1)
a₂₂=-98+2*21
a₂₂=-54
а(n)=7 ?
7=-98+2(n-1)
7=2n-100
2n=107
n=53.5 - не является натуральным числом, значит число 7 не является членом арифметической прогрессии: -98; -96...
Объяснение:
1.
а)
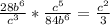
б)
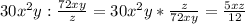
в)
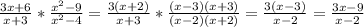
г)
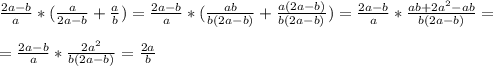
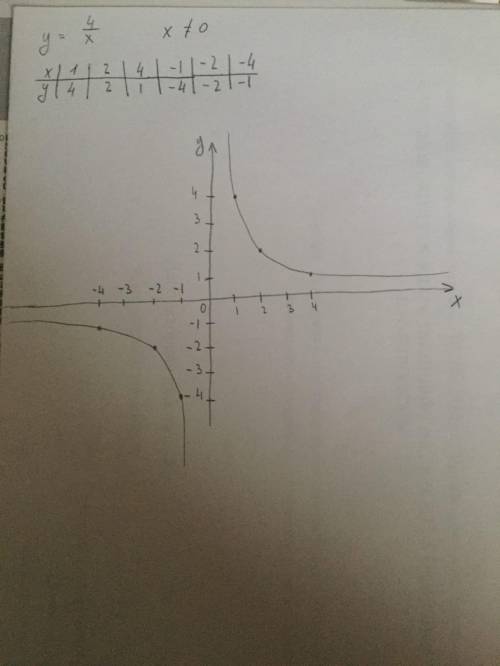
2. График на фото.
Область определения:
D(f)=(-∞;0)∪(0;+∞)
Функция принимает положительные значения при всех положительных Х, кроме 0(так как при нем знаменатель будет равен нулю).
3.
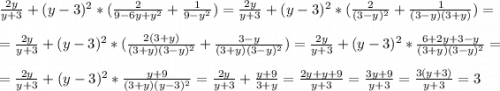
Получаем, что при всех значениях Y(кроме +-3) значение выражение будет равно 3, то есть какой бы Y мы не взяли, данное выражение всегда будет давать в ответе 3, что говорит о том, что оно не зависит от Y.
4.
Данное выражение имеет смысл при всех Х, кроме тех, при которых знаменатель будет равен 0.
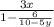
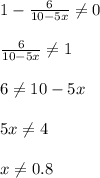
x∈(-∞;0.8)∪(0.8;+∞)
1.N=1 7^2+8=57, 57/19=3 - верно
2. Предположим что n=k, 7^(k+1) + 8^(2k-1) кратно 19, тогда докажем тоже для n=k+1
7^(k+2)+8^(2k+1)=
7*7^(k+1)+64*8^(2k-1)=
7*7^(k+1)+7*8^(2k-1)+57*8^(2k-1)=
7*(7^(k+1)+8^(2k-1))+57*8^(2k-1)
Произведение нат. чисел кратно какому-либо числу если 1 из его множителей кратен этому числу, первое слагаемое делится на 19 по предположению вначале пункта 2, а второе слагаемое кратно 19, т.к. 57 кратно 19
Доказано.