ответ: y= -3x+11 .
Уравнение функции, описывающей прямо пропорциональную зависимость между переменнными "х" и "у" , такая:  .
.
Подставим координаты точки А(-4;12) в это равенство и найдём коэффициент k .
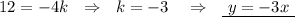
Линейная функция задаётся уравнением 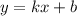 .
.
Так как график линейной функции параллелен графику прямой пропорциональности, то у этих функций будут равные угловые коэффициенты, то есть линейная функция будет иметь вид 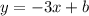
Найдём число "b" , подставив координаты точки D(7;-10) в уравнение линейной функции.
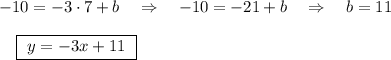
ответ: y= -3x+11 .
Уравнение функции, описывающей прямо пропорциональную зависимость между переменнными "х" и "у" , такая:  .
.
Подставим координаты точки А(-4;12) в это равенство и найдём коэффициент k .
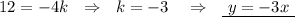
Линейная функция задаётся уравнением 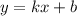 .
.
Так как график линейной функции параллелен графику прямой пропорциональности, то у этих функций будут равные угловые коэффициенты, то есть линейная функция будет иметь вид 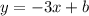
Найдём число "b" , подставив координаты точки D(7;-10) в уравнение линейной функции.
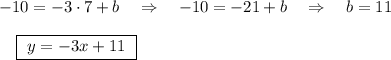
7х^2+13x-2<0
D=15^2
X1=1\7
X2=-2
7х^2+13x-2=(X-1\7)(X+2)
(X-1\7)(X+2)<0
Получаем:
отсюда x будет принадлежать: (-2;1/7).
Но на этом решение не заканчивается, т.к. мы решили только первое неравенство СИСТЕМЫ неравенств.
Чтобы решить систему неравенств, нам потребуется найти все общие решения всех уравнения\неравенства системы или установить, что их нет.
Второе неравенство системы это X>0.
Находим объединение этих решений:
Х принадлежит промежутку (0;1/7)