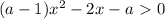
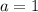 , то получим линейное неравенство:
, то получим линейное неравенство: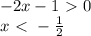
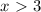 .
.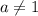 - имеем квадратное неравенство.
- имеем квадратное неравенство. 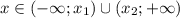
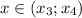
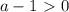 , тогда
, тогда 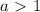
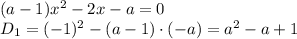
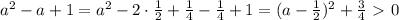
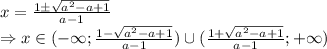
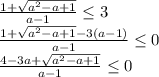
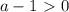 , то можно перейти к следующему неравенству:
, то можно перейти к следующему неравенству:![4-3a+\sqrt{a^2-a+1} \leq 0 \\\ \sqrt{a^2-a+1} \leq 3a-4 \\\ \begin{cases} a^2-a+1 \leq (3a-4)^2 \\ 3a-4\ \textgreater \ 0 \right \end{cases} \\\ \begin{cases} a^2-a+1 \leq 9a^2-24a+16 \\ 3a\ \textgreater \ 4 \right \end{cases} \\\ \begin{cases} 8a^2-23a+15 \geq 0 \\ a\ \textgreater \ \frac{4}{3} \right \end{cases} \\\ \begin{cases} a\in(-\infty;1]\cup[ \frac{15}{8} ;+\infty) \\ a\ \textgreater \ \frac{4}{3} \right \end{cases}](/tpl/images/0507/6430/22606.png)
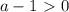 :
: 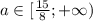
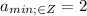
Объяснение:
К 1 января 20951 г. жители получат:
1,3*0,07 = 0,091 млн = 91 тыс золотых.
И уже с этих процентов они могут купить досок на 79 тыс золотых.
В 20952 году, с 1 января до 1 июля, за 7 месяцев они получат:
91*7/12 = 53,0833 тыс ≈ 53 тыс золотых.
Всего за 2 года они получат:
91 + 53 = 144 тыс золотых.
После покупки у них останется:
144 - 79 = 65 тыс золотых.
ответ: 144 тыс получат, 65 тыс останется, они смогут купить доски.
А если в 20951 году дракон ещё награбит, то можно пересчитать сумму, и тогда на 2-ой год жители получат ещё больше.
2) y = 19Х + 5
3) y = 36Х - 40 или -y = -36Х + 40
4) y = -15Х + 53