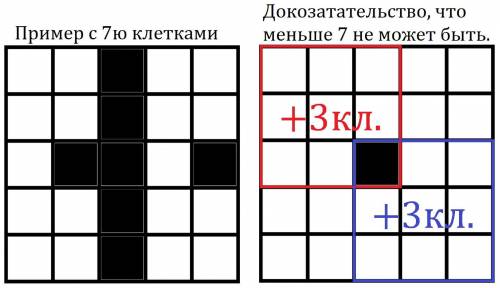
![x^2-1 \leq 0, \\ (x+1)(x-1) \leq 0, \\ (x+1)(x-1) = 0, \\ x_1=-1, x_2=1, \\ -1 \leq x \leq 1, \\ x\in[-1;1]](/tpl/images/0305/1311/503a6.png)
![x^2-9 \geq 0, \\ (x+3)(x-3) \geq 0, \\ (x+3)(x-3) = 0, \\ x_1=-3, x_2=3, \\ \left [ {{x \leq -3,} \atop {x \geq 3;}} \right. \\ x =\in(-\infty;-3]\cup[3;+\infty).](/tpl/images/0305/1311/c69fe.png)
![x^2+x-6 \leq 0, \\ x^2+x-6 = 0, \\ x_1=-3, x_2=2, \\ -3 \leq x \leq 2, \\ x\in[-3;2].](/tpl/images/0305/1311/1fdfa.png)
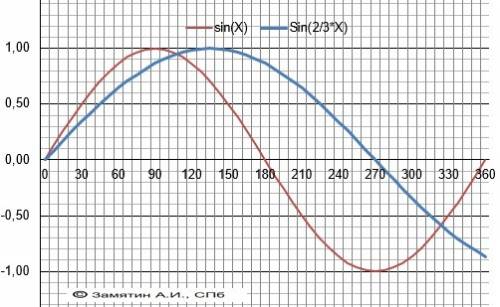
ответ: 7.
Объяснение:
Смотри первое приложение. Закрасим 7 клеток чтобы выполнялось условие (лев. квадрат 5х5). Докажем, что меньше семи клеток быть не может (прав. квадрат 5х5). Рассмотрим два квадрата 3х3 (красн. и син.). Чтобы количество закрашенных клеток было минимальным, необходимо закрасить все общие клетки этих квадратов (1 центральная). Видим, что для двух этих квадратов необходимо закрасить ещё по 3 клетки, чтобы всего было по 4. Тогда минимальное количество клеток 1+3+3=7, что и требовалось доказать. Во втором приложении я рассмотрел каждый квадрат 3х3, чтобы показать правильность расстановки.