Алгебра: Решить с разъяснениями (2√3-√5)(2√3+√5)

Решить с разъяснениями (2√3-√5)(2√3+√5)

👇

Увидеть ответ

Ответ:

gggggerrrr

21.03.2023

$(2\sqrt{3}-\sqrt{5})(2\sqrt{3}+\sqrt{5})=$
используем формулу разности квадратов (a-b)(a+b)=a^2-b^2

= $(2\sqrt{3})^2-(\sqrt{5})^2=$
используем формулу степени произведения (ab)^n=a^nb^n

= $2^2*(\sqrt{3})^2-(\sqrt{5})^2=$
используем формулу $(\sqrt{a})^2=a$
=4*3-5=12-5=7
ответ: 7

4,6(85 оценок)

Открыть все ответы

Ответ:

Sashapro111

21.03.2023

Объяснение:

построить график функции и описать свойства у=2(х-3)(х+1)

Точки пересечения с осью Х

х-3=0 х=3

х+1=0 х=-1 вершина лежит посредине этого отрезка.

Значит Х вершины=(3-1)/2=1 У вершины равен 2(1-3)(1+1)= -8

У этой параболы ветви вверх (поскольку х*х не имеет минуса перед собой),значит есть минимум в вершине (1;-8). Ось у пересекается в точке 2(0-3)(0+1)=6 (0;-6)

Функция убывает слева от вершины х∠1

возрастает справа от вершины 1∠х

отрицательные значения при х между точками пересечения с осью Х. (нижняя часть параболы под осью) -1∠х∠3

Положительные значения при Х правее правой и левее левой точки.

х∠-1 или 3∠х функция положительная.

график строим симметрично оси ,проходящей через вершину. имеем точку вершины (1;-8) точку на оси у (0;-6) точку на оси х.(-1;0) справа имеем точку на оси х=3 точка 0;-6 на 1 клеточку левее оси,значит такая же точка будет и справа. (2;-6) плавно соеденяешь эти точки,получаешь график.

4,5(39 оценок)

Ответ:

StacyZviozdohkina

21.03.2023

Так как AK - биссектриса, то:
$\frac{BK}{AB}= \frac{KC}{AC} \ \ \textless \ =\ \textgreater \ \ \frac{BK}{KC}= \frac{AB}{AC}$
при делении точкой отрезка на 2 части, относящиеся как m к n, есть формула для вычисления координат этой точки:
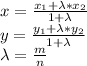
$x= \frac{x_1+\lambda*x_2}{1+\lambda}
\\y= \frac{y_1+\lambda*y_2}{1+\lambda}
\\\lambda= \frac{m}{n}$
ищем длины AB и AC:
используем формулу:
$|AB|=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$
$|AB|=\sqrt{(-2-2)^2+(5-2)^2}=\sqrt{16+9}=5
\\|AC|=\sqrt{(-2-10)^2+5^2}=\sqrt{169}=13$
$\frac{BK}{KC}= \frac{AB}{AC}= \frac{5}{13} =\lambda$
находим координаты точки K:
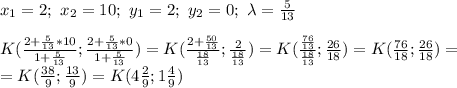
$x_1=2;\ x_2=10;\ y_1=2;\ y_2=0;\ \lambda=\frac{5}{13}
\\
\\K( \frac{2+ \frac{5}{13}*10 }{1+\frac{5}{13}} ;\frac{2+ \frac{5}{13}*0 }{1+\frac{5}{13}})=K( \frac{2+ \frac{50}{13} }{ \frac{18}{13}}; \frac{2}{ \frac{18}{13} })=K( \frac{ \frac{76}{13} }{ \frac{18}{13}}; \frac{26}{18} )=K( \frac{76}{18}; \frac{26}{18}) =
\\=K( \frac{38}{9}; \frac{13}{9})=K(4 \frac{2}{9};1 \frac{4}{9} )$
теперь определим вид треугольника для этого используем теорему косинусов:
для начала найдем длину BC:
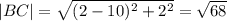
$|BC|=\sqrt{(2-10)^2+2^2}=\sqrt{68}$
вид треугольника будем определять по косинусу самого большого угла; если cos<0, то угол тупой; если cos=0, то угол прямой; если cos>0, то угол острый.
Против большей стороны лежит больший угол, поэтому запишем теорему косинусов для AC и косинуса угла B
$AC^2=AB^2+BC^2-2*AB*BC*cosB
\\2*AB*BC*cosB=AB^2+BC^2-AC^2
\\cosB= \frac{AB^2+BC^2-AC^2}{2*AB*BC}$
подставим значения:
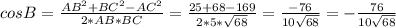
$cosB= \frac{AB^2+BC^2-AC^2}{2*AB*BC}= \frac{25+68-169}{2*5*\sqrt{68}}= \frac{-76}{10\sqrt{68}} =- \frac{76}{10\sqrt{68}}$
cosB<0 поэтому угол тупой и треугольник тупоугольный
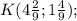ответ: $K(4 \frac{2}{9};1 \frac{4}{9} );\$ треугольник тупоугольный