(-бесконечности ; -10] и (7; +бесконечности)
Объяснение:
Запишем все под одной дробью:
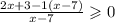
Найдём область допустимых значений:
х-7≠0, то есть х ≠ 7
Раскроем скобки и решим:
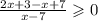
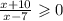
Рассмотрим все возможные случаи (знаменатель строго больше нуля, так как если он будет равен нулю, выражение потеряет смысл):
1. Когда и знаменатель, и числитель больше 0
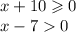
2. Когда оба меньше 0
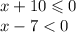
1.
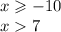
То есть х принадлежит ( 7; +бесконечности)
Так как 7 не удовлетворяет ОДЗ, то скобки круглые
2.
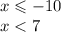
То есть х принадлежит (- бесконечности ; - 10]
Найдём объединение:
Х принадлежит (-бесконечности ; -10] и (7; +бесконечности)
1) 2y^2/x^5
2)(2m^2)/(m+5)
Объяснение:
1) Запишем частное, как произведение одной дроби на перевернутую другую:
(16х^3*у^6)/(y^4*8x^8)
Сократим на 8:
(2х^3*y^6)/(y^4*x^8)
Найдем х и у с минимальными степенями - это х в третьей и у в четвертой. Сократим на них:
2y^2/x^5
Сокращать больше нечего. Это ответ.
2) Вынесем из числителя первой дроби m:
(m(m+5))/5
Разложим числитель второй дроби по формуле разности квадратов*:
*(a+b)(a-b)=a^2-b^2
((m-5)(m+5))/10m
Запишем частное, как произведение одной дроби на перевернутую другую:
(m(m+5)*10m)/(5(m-5)(m+5))
Сократим на (m+5):
(10m^2)/(5(m-5))
Сократим на 5:
(2m^2)/(m-5)
Сокращать больше нечего. Это ответ.
Вибачте за рішення російською, не говорю українською. Сподіваюся, що допоміг! :)
а) 1/2 : 1/4 : 1/4 = 2 : 1 : 1
4/2 : 4/4 : 4/4 = 2 : 1 : 1 (умножили на 4)
б) 1 1/3 : 1 1/2 : 1 = 8 : 9 : 6
4/3 : 3/2 : 1 = 24/3 : 18/2 : 6/1 = 8 : 9 : 6 (умножили на 6)
в) 0,5 : 1 : 1,5 = 1 : 2 : 3 (умножили на 2)
г) 4,5 : 2,7 : 1,8 = 45 : 27 : 18 (умножили на 10)