А - попадание первого баскетболиста
В - попадание второго баскетболиста.
Имеем три случая
1) Если у первого баскетболиста три попадания, а у второго меньше 3 попадания
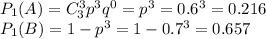
Вероятность того, что у первого баскетболиста три попадания,а у второго меньше трех попадания, равна 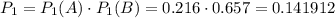
2) Если у первого баскетболиста 2 попадания, а у второго 0 или 1.
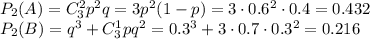
По теореме умножения, вероятность того, что первый баскетболист попадет 2 раза, а второй - 0 или 1, равна 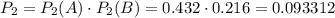
3) Если у первого баскетболиста одно попадание, то у второго 0 попаданий
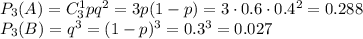
Вероятность того, что первый попадет один раз, а второй ниразу, равна
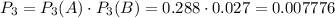
По теореме сложения, вероятность того, что у первого баскетболиста будет больше попаданий, чем у второго, равна
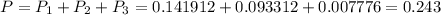
ответ: 0,243.
Нужно доказать, что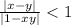
так как левая и правая части неотрицательны, это неравенство равносильно следующему (поднесем обе части к квадрату, чтобы избавиться от модуля так как |a|^2=a^2)
так как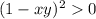 (0 не может быть потому что знаменатель не может быть равным 0, а квадрат выражения всегда неотрицателен),
(0 не может быть потому что знаменатель не может быть равным 0, а квадрат выражения всегда неотрицателен),
то нужно доказать что справедливо неравенство
то справедливо так как (y^2-1<0; y^2<1; |y|<1) (|x|<1; x^2<1; 1-x^2>0)
(один из множителей отрицателен, другой положителен - значит и произведение отрицательное).
Таким образом цепочкой равносильных преобразований мы пришли к справедливому неравенству. Доказано