DE – радиус данной окружности.
Возьмём точку К (4;-7), проведем по линиям клеток DK и EK.
DK=|-5–(-7)|=|-5+7|=2
EK=|4–(-2)|=|4+2|=6
Так как углы любой клетки равны 90°, то угол DKE=90°.
Тогда по теореме Пифагора в ∆DKE:
DE²=DK²+EK²
DE²=2²+6²
DE²=4+36
DE²=40
То есть квадрат радиуса окружности равен 40.
Уравнение окружности имеет вид:
(x–a)²+(y–b)²=R²
где кординаты центра окружности (а;b), а R – радиус.
a) Центр окружности – точка D имеет кординаты (4;-5), тогда получим уравнение:
(x–4)²+(y+5)²=40
b) Центр окружности – точка E имеет кординаты (-2;-7), получим уравнение:
(х+2)²+(у+7)²=40
ответ выделен жирным шрифтом. Так как не дано какая из двух точек центр, я расписал два случая. Но вероятнее что всё-таки случай а)
Тогда ответ: (x–4)²+(y+5)²=40
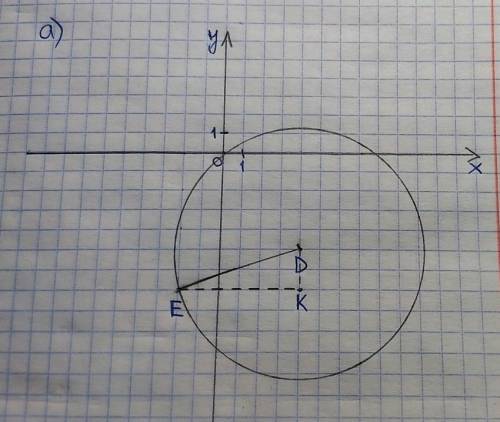
ответ: V=a³•sin²α•tgβ/6
Объяснение - очень подробно:
Формула объема пирамиды V=S•h/3, где S – площадь основания пирамиды, h - её высота.
Стороны ромба равны. По условию боковые грани наклонены к плоскости основания под углом β.
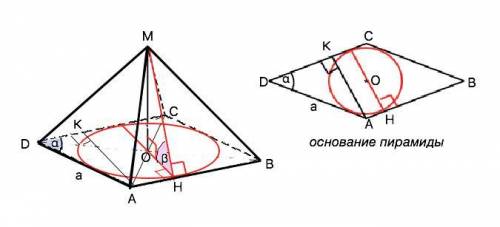
Если боковые грани пирамиды наклонены к плоскости основания под одним углом, то в основание пирамиды можно вписать окружность, а вершина пирамиды проецируется в центр этой окружности.
Центр окружности, вписанной в ромб – точка пересечения его диагоналей, а расстояние от него до сторон равно радиусу вписанной окружности.
Высота пирамиды, радиус вписанной окружности и высота боковой грани образуют прямоугольный треугольник, при этом высота боковой грани и радиус вписанной окружности образуют линейный угол между основанием и боковой гранью, т.к. по т. о 3-х перпендикулярах перпендикулярны стороне ромба (ребру двугранного угла) в одной точке.
Диаметр окружности, вписанной в ромб, перпендикулярен его сторонам, параллелен высоте ромба и равен ей. На рисунке приложения АК = высота ромба. АК=АD•sinα=a•sinα ⇒ HO=r=a•sinα•1/2. Из прямоугольного ∆ МОН высота пирамиды МО=ОН•tgβ=(a•sinα•1/2)tgβ
S(ABCD)=AD•CD•sinα=a²•sinα
V=a²•sinα•(a•sinα•1/2)tgβ/3=a³•sin²α•tgβ/6
Через точку А проведём плоскость, параллельную заданной.
Общее уравнение заданной плоскости имеет вид:
Ax+By+Cz+D=0 (2)
Все параллельные плоскости имеют коллинеарные нормальные векторы. Поэтому для построения параллельной к (2) плоскости, проходящей через точку M0(x0, y0, z0) нужно взять в качестве нормального вектора искомой плоскости, нормальный вектор n=(A, B, C) плоскости (2). Далее нужно найти такое значение D, при котором точка M0(x0, y0, z0) удовлетворяла уравнению плоскости (2):
Ax0+By0+Cz0+D=0. (3)
Решим (3) относительно D:
D=−(Ax0+By0+Cz0) (4)
Из уравнения (1) запишем координаты нормального вектора :
A= 1 , B= 1 , C= −1 .
Подставляя координаты точки А и координаты нормального вектора в (4), получим:
D=−(Ax0+By0+Cz0)=− 1 · 1 + ( −1) · 1 + 1 · (−1) = 1
Подставляя значения A, B, C, D в (2), получим уравнение плоскости, проходящей через точку А(1, -1, 1) и параллельной плоскости (1):
x+ y − z+ 1 =0.
Теперь найдём точку пересечения новой плоскости с заданной прямой.
Надо решить систему, разложив уравнение прямой:
{x+ y − z+ 1 =0,
{x = 2y - 6,
{z = -y + 3.
Подставим в первое уравнение x и z:
2y - 6 + y + y - 3 + 1 = 0,
4y = 8,. y = 8/4 = 2.
x = 2*2 - 6 = -2,
z = -2 + 3 = 1.
Получили уравнение точки Р, лежащей в плоскости, параллельной заданной: Р(-2; 2; 1). Вектор АР(-3; 3; 0).
Воспользуемся формулой канонического уравнения прямой:
x - xa xb - xa = y - ya yb - ya = z - za zb - za
Так как: zb - za = 0, то уравнение прямой в каноническом виде записать нельзя.
Составим параметрическое уравнение прямой
Воспользуемся формулой параметрического уравнения прямой:
x = l t + x1
y = m t + y1
z = n t + z1
где:
{l; m; n} - направляющий вектор прямой, в качестве которого можно взять вектор AB;
(x1, y1, z1) - координаты точки лежащей на прямой, в качестве которых можно взять координаты точки A.
AB = {xb - xa; yb - ya; zb - za} = {-2 - 1; 2 - (-1); 1 - 1} = {-3; 3; 0}
В итоге получено параметрическое уравнение прямой:
x = - 3t + 1
y = 3t - 1
x = 1.