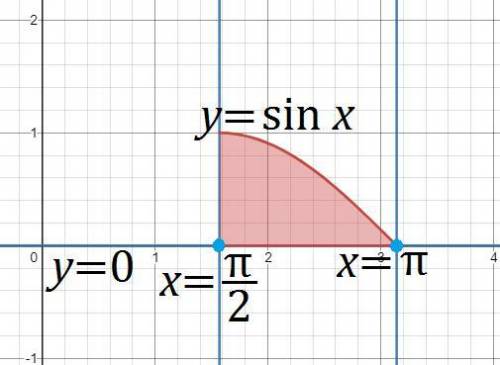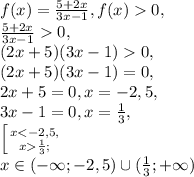
18 дней и 36 дней
Объяснение:
х - скорость работы первой бригады
у - скорость работы второй бригады
Всю работу примем за 1.
По условию, работая вместе бригада выполнит работу за 12 дней, значит 1/(х+у)=12.
Первая бригада выполнит половину работу 1/(2х) и вторая работа выполнит оставшуюся часть, т.е. половину работы 1/(2у) за 27 дней.
Составим и решим систему уравнений:
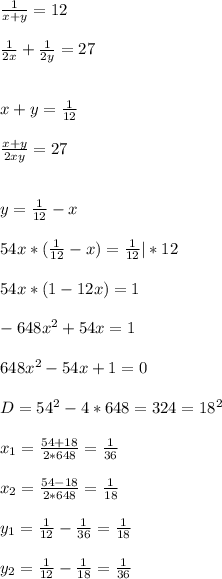
Т.е. скорость одной бригады 1/18, а скорость другой 1/36
1:1/18=18 дней потребуется одной бригаде на выполнение всей работы
1:1/36=36 дней потребуется другой бригаде для выполнения всей работы
1. 2)
2. 3)
Объяснение:
1. 
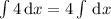, интеграл 
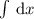табличный и равняется 
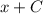, тогда исходный равняется 
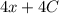, произведение констант — тоже константа, поэтому решением будет 
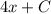, что соответствует второму варианту ответа.
2. Область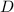 
, ограниченная указанными кривыми 
, 
, 
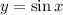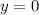и 
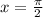, показана на приложенном рисунке. Получается, что 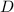задают два неравенства, 
и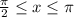 
. Первое неравенство задаёт подынтегральную функцию, притом напрямую (так как левая часть неравенства равна нулю), а второе — пределы интегрирования.
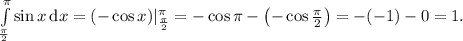
(Так получается, ибо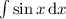 
— табличный интеграл, равный 
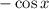, а затем для определённого интегрирования применяется формула Ньютона-Лейбница, то есть 
, при известном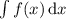 
, то есть 
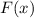, притом константа в таком случае игнорируется.)
Полученный результат соответствует третьему варианту ответа.
