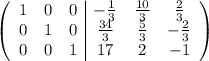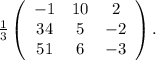
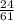 проте ймовірність того, що листок містить саме число 2 менша та дорівнює
проте ймовірність того, що листок містить саме число 2 менша та дорівнює 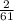
Объяснение:
У високостном році 366, є місяці по 31 денів по 30 днів та у лютому 29 днів
Тож подивимось скількі днів у місяці містять двійку:
це номери 2, 12, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29 - загалом це 12 днів на місяць,
як бачимо у кожному місяці високостного року по 12 днів із цифрою 2
тому на рік таких днів буде 12*12=144
а ймовірність такої події 
--------------------------
якщо ж казати про можливість натрапити саме на число 2 на листочку то це лише  , оскыльки других днів у році стількиж скіль ки ж і місяців у році, а саме
, оскыльки других днів у році стількиж скіль ки ж і місяців у році, а саме 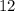
Пусть  - канонический базис в
- канонический базис в 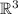 .
.
Тогда матрицу перехода 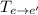 можно найти следующим образом:
можно найти следующим образом:
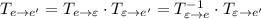
Если записать блочную матрицу 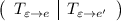 и привести путем элементарных преобразований к виду
и привести путем элементарных преобразований к виду  , то
, то 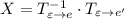
Матрицу 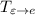 легко получить: достаточно записать в столбцы координаты векторов базиса
легко получить: достаточно записать в столбцы координаты векторов базиса  . Аналогично с матрицей
. Аналогично с матрицей  .
.
В итоге необходимо получить вид  следующей матрицы:
следующей матрицы:
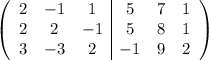
Вычтем первую строку из второй и третьей:
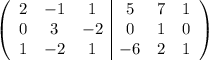
Вычтем из первой строки 2 третьих и поменяем их местами:
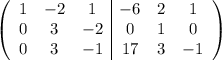
Вычтем из третьей строки вторую:
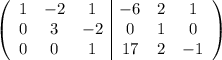
Прибавим ко второй строке 2 третьих и вычтем из первой третью:

Делим вторую строку на 3:
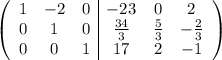
Прибавляем в первой строке 2 вторых: