
Определения. Углом между прямыми A и B называется угол, на который надо повернуть первую прямую A вокруг точки пересечения этих прямых против движения часовой стрелки до совпадения ее со второй прямой B. Если две прямые заданы уравнениями с угловым коэффициентом, то угол между ними определяется по формуле:
tgψ = (k2-k1)/(1+k1*k2). (1)
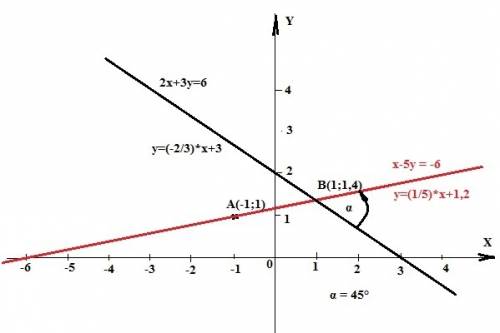
Нам задано уравнение первой прямой, угол между прямыми: ψ = 45° и точка А(-1;1), через которую проходит вторая прямая. Эта прямая будет единственной по определению угла между прямыми.
Запишем уравнение первой прямой в виде уравнения с угловым коэффициентом: y = -(2/3)+3 (2). k=-2/3. Найдем угловой коэффициент второй прямой по формуле (1), зная, что тангенс 45° = 1:
1=(k2+2/3)/(1+(2/3)*k2) => (5/3)*k2=1/3 => k2 = 1/5.
Если известна точка A(-1;1) , принадлежащая некоторой прямой, и угловой коэффициент этой прямой, то уравнение данной прямой выражается формулой: Y - Ya = k(X - Xa). В нашем случае:
Y - 1 = (1/5)*(X+1) => Y=(1/5)*X+6/5 (уравнение с угловым коэффициентом). Или x - 5y +6 = 0 (уравнение в общем виде). Или x-5y= -6.
ответ: уравнение прямой, проходящей через точку А(-1;1) под углом 45° к прямой 2х+3у=6: x-5y= -6.
sin 2x = 2 sinx * cos x
выносим из числителя 2 sinx. lim(x->0) 2 sinx/ х = 2
осталось вычислить lim(x->0) [cos x - 1 ] / ln cos(5x) неопределенность 0 на 0.
Проще всего по Лопиталю - вычислить производные числителя и знаменателя
Без Лопиталя
cos x -1 = - 2 sin^2 (x/2)
ln cos(5x) = ln [1+ ( cos 5x - 1) ] = ln [ 1- 2 sin^2 (5x/2) ]
---> - 2 sin^2 (5x/2)
после подстановки имеем
lim(x->0) { - 2 sin^2 (x/2) } / { - 2 sin^2 (5x/2) } = lim(x->0) { x^2/4 * [ sin^2 (x/2) / (x/2)^2} / { 25 x^2/4 * [sin^2 (5x/2)/(5x/2)^2 }=
= lim(x->0) { x^2 / 25 x^2 } =1/25
[ sin^2 (x/2) / (x/2)^2}=1 [sin^2 (5x/2)/(5x/2)^2 =1
1+ (cos^4t+sin^2tcos^2t)/sin^2t=1/sin^2t 1+ cos^2t(cos^2t+sin^2t)/sin^2t=1/sin^2t 1+ cos^2t/sin^2t=1/sin^2t (cos^2t+sin^2t)/sin^2t =1/sin^2t 1/sin^2t =1/sin^2t 1=1 тождество доказано.