Если известны длины двух векторов и угол между ними, то подсчитайте сумму квадратов длин векторов a и b, и прибавьте к ней их удвоенное произведение, умноженное на косинус угла α между ними. Из полученного числа извлеките корень квадратный c=√(a²+b²+2∙a∙b∙cos(α)). Это будет длина вектора, равного сумме векторов a и b.
с = √(16 + 81 + 2 * 4 * 9 * -0,5) = 7,81.
Проверяйте вычисления.

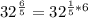
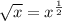
![\sqrt[3]{x} =x^{\frac{1}{3}}](/tpl/images/0503/0859/f093d.png)
![32^{ \frac{1}{5}} =\sqrt[5]{32}](/tpl/images/0503/0859/6c7d6.png)
![\sqrt[5]{32}=\sqrt[5]{2^{5}}](/tpl/images/0503/0859/ad486.png)
![\sqrt[5]{2^{5}}=2^{\frac{5}{5}}=2](/tpl/images/0503/0859/67bfa.png)
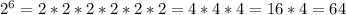
Чтобы решить это нужно |a+c| поднести к квадрату. Тогда:
То есть: |a+c|=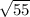 .
.
ответ: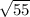 .
.