Сторона данного треугольника а(3) равна Р:3=6√3:3=2√3 дм
Формула радиуса окружности, описанной около правильного треугольника:
R=a/√3 =>
R=2√3:√3=2 дм
Формула стороны правильного многоугольника через радиус вписанной окружности:
а(n)=2r•tg(180°:n), где r – радиус вписанной окружности, n – число сторон,
Для правильного шестиугольника tg(180°:n)=tg30°=1/√3
a₆=2•2•1/√3=4/√3
P=6•4/√3=8√3 дм
—————
Как вариант: Правильный шестиугольник состоит из 6 равных правильных треугольников.
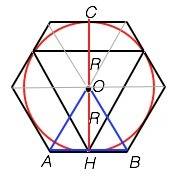
На рисунке приложения ОН - радиус описанной около правильного треугольника окружности и в то же время высота одного из 6 правильных треугольников, все углы которого 60°; АВ - сторона шестиугольника. Задача решается с т.Пифагора.
25^x + (4/25^x) - ( 5^x + (2/5^x) ) <= 2,
25^x + (4/25^x) = (5^x)^2 + (2/5^x)^2 = (5^x)^2 + 4 + (2/5^x)^2 - 4 =
= ( 5^x + (2/5^x) )^2 - 4.
сделаем замену переменной 5^x + (2/5^x) = t.
Тогда получим следующее неравенство:
t^2 - 4 - t <= 2,
t^2 - t - 6 <=0,
t^2 + 2t - 3t - 6 <=0,
t*(t+2) - 3*(t+2) <=0,
(t+2)*(t-3) <=0,
Решая это неравенство найдем, что -2<=t<=3.
Теперь делаем обратную замену переменной и нужно решить систему из двух неравенств:
5^x + (2/5^x) >= -2,
5^x + (2/5^x) <=3.
1) 5^x + (2/5^x) >= -2, домножаем на 5^x >0,
5^(2x) + 2*5^x + 2 >=0,
( 5^x + 1)^2 + 1 >=0, верно для всех икс.
2) 5^x + (2/5^x) <=3, домножаем на 5^x >0,
5^(2x) - 3*5^x + 2 <=0,
опять делаем замену 5^x = u,
u^2 - 3u + 2 <=0,
u^2 - u - 2u + 2 <=0,
u*(u-1) - 2*(u-1) <=0,
(u-1)*(u-2) <=0,
решая это квадратное неравенство найдем, что
1<=u<=2
делаем обратную замену
1<=5^x <=2,
Получаем систему неравенств:
5^x >=1,
5^x <= 2.
1) 5^x >=1,
5^x >= 5^0,
x>=0.
2) 5^x <= 2 = 5^log_5(2),
x<= log_5(2).
Итак, 0<= x<=log_5(2) .