Объяснение:
a) (3ab + 5a - b) - (12ab - 3a) = 3ab + 5a - b - 12ab + 3a = 8a - b - 9ab
б) 2x²·(3 - 5x³) = 6x² - 10x⁵
в) (2a - 3c)(a + 2c) = 2a² + 4ac - 3ac - 6c² = 2a² + ac - 6c²
г) (y - 1)(y² + 2y - 4) = y³ + 2y² - 4y - y² - 2y + 4 = y³ + y² - 6y + 4
д) (3x³ - 6x²) ÷ (3x²) = 3x²·(x - 2) / (3x²) = x - 2
a) (3·a·b + 5·a - b) - (12·a·b - 3·a) = 3·a·b + 5·a - b - 12·a·b + 3·a = 8·a - b - 9·a·b ;
б) 2·x²·(3 - 5·x³) = 6·x² - 10·x⁵ ;
в) (2·a - 3·c)·(a + 2·c) = 2·a² + 4·a·c - 3·a·c - 6·c² = 2·a² + a·c - 6·c²;
г) (y - 1)·(y² + 2·y - 4) = y³ + 2·y² - 4·y - y² - 2·y + 4 = y³ + y² - 6·y + 4 ;
д) (3·x³ - 6·x²) : (3·x²) = 3·x²·(x - 2) : (3·x²) = x - 2.
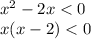
Решаем с метода интервалов: 1). для этого все выражения с х приравниваем к нулю и решаем полученные уравнения (х=0, х= 2);
2). определяем точки, которые соответствуют найденным нулям и отмечаем их выколотыми точками (т.к. неравенство строгое) на оси координат;
3). определяем знаки выражения f(x)
из левой части решаемого неравенства на каждом промежутке и проставляем их на графике;
4). наносим штриховку над нужными участками графика, руководствуясь следующим правилом: в случае, если неравенство имеет знак <, то изображается, штрихуются «минусовые» промежутки.
5). Заштихованный промежуток и будет являться ответом.
ответ: (0;2).
64%
Объяснение:
staranja
Пусть ученик хочет купить на x рублей ручек и на y рублей карандашей.
Стоимость этой покупки берём за 100%.
Если карандашей будет y/2, то стоимость покупки будет 100 - 34 = 66% от задуманной.
x + y = 100
x + y/2 = 66
100 - y = 66 - y/2
34 = y/2
y = 68% - стоимость всех карандашей составляет 68% покупки.
Тогда стоимость всех ручек составляет 100 - 68 = 32% покупки.
Если ученик возьмёт в три раза больше ручек, то к стоимости покупки прибавится дважды по 32%.
32 * 2 = 64%
ответ: стоимость покупки возрастёт на 64%.
а) (3ab + 5a – b) – (12ab – 3a)=3ab+5a-b-12ab+3a=8a-b-9ab
б) 2х2(3 – 5х3)= если 2x * 2*(3-5x*3) to 4x*(3-15x)=12x-60x^2
если 2x в квадрате то 2x^2(3-5x^3)=6x^2-10x^5
в) (2а – 3с)(а + 2с)=2a^2+4ac-3ac-6c^2=2a^2+ac-6c^2
г) (у – 1)(у2 + 2у – 4)=y^3 + 2y^2 - 4y - y^2 - 2y + 4=y^3 + y^2 - 6y + 4
д) (3х3 – 6х2): 3х2=3x^2(x-6)/3x^2=x-6
^-знак возведения в степень