Question

Укажите позволяющий установить взаимно однозначное соответствие: а) между множеством четных натуральных чисел и множеством нечетных натуральных чисел; б) множеством квадратов натуральных чисел и множеством кубов натуральных чисел.

Answer 1

а)

Множество четных натуральных чисел: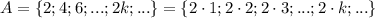 $A=\{2;4;6;...;2k;...\}=\{2\cdot1;2\cdot2;2\cdot3;...;2\cdot k;...\}$

Множество нечетных натуральных чисел: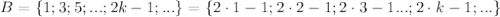 $B=\{1;3;5;...;2k-1;...\}=\{2\cdot1-1;2\cdot2-1;2\cdot3-1...;2\cdot k-1;...\}$

Можно заметить, что если от любого элемента множества А отнять 1, то получится элемент множества B.

Тогда, если x - четное натуральное число, y - нечетное натуральное число, то:

$y=x-1$

б)

Множество квадратов натуральных чисел: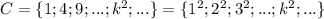 $C=\{1;4;9;...;k^2;...\}=\{1^2;2^2;3^2;...;k^2;...\}$

Множество кубов натуральных чисел: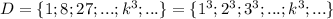$D=\{1;8;27;...;k^3;...\}=\{1^3;2^3;3^3;...;k^3;...\}$

Можно заметить, что если из любого элемента множества C извлечь квадратный корень и получившееся число возвести в куб, то получится элемент множества D.

Тогда, если x - квадрат натурального числа, y - куб натурального числа, то:

$y= \sqrt{x^3}$